Количество счастливых билетов формула – Задача о счастливых билетах :: Производящие функции

Содержание

Число «счастливых’’ билетов | Математика, которая мне нравится

Сначала немного истории. Автобусные билеты имели (да и сейчас это, кажется, так же) номера, состоящие из шести цифр. Разумеется, номер билета мог начинаться на . “Счастливыми’’ назывались билеты, у которых сумма первых трех цифр равна сумме последних трех цифр. Была распространена уверенность (во всяком случае, среди детского населения страны), что если тебе достался “счастливый’’ билет, ты можешь загадать желание и съесть билет, тогда твое желание исполнится. Отсюда название. Конечно же, “счастливые’’ билеты доставались ребятишкам не так уж часто. Честно говоря, ни разу не видела, чтобы кто-нибудь такой билет действительно съел, да и сама не ела. Хотя слухи о съевших “счастливый’’ билет и взамен получивших исполнение желания, ходили, и многие были убеждены в том, что они основаны на реальных событиях Соответственно, поскольку билетов таких было не так уж много, возникла и следующая задача о числе “счастливых’’ билетов. Итак,

задача. Каждый из миллиона билетов пронумерован последовательностью из шести цифр (от до ). Сколько существует билетов, у которых сумма первых трех цифр равна сумме последних трех цифр?

В наше время эта задача была достаточно известной. Мне, помнится, она была предложена на уроке алгебры в 9 классе, когда изучали комбинаторику. Кроме того, на тему “счастливых’’ билетов были статьи в журнале “Квант’’ (например, их можно найти здесь). Но удивительно то, что сейчас почему-то пишут о других методах подсчета числа “счастливых’’ билетов, совсем не о комбинаторных, как это было раньше. В основном предлгается программа, написанная на одном или другом языке программирования, которая позволяет решить эту задачу. Забавно, что в написании такой программы ничего сложного нет, это всего лишь цикл, т.е. вещь достаточно стандартная и скучная. А вот попытаться решить задачу с помощью комбинаторики гораздо интереснее и полезнее. Надеюсь, вы это сделаете, прежде чем начать читать дальше .

Решение.

Само решение требует достаточно большого числа вычислений, однако они не очень сложные. Важно понять, как их сократить.

Найдем — число билетов, у которых сумма первых трех цифр равна сумме трех последних цифр и равна . Ясно, что может принимать значения от (три ) до (три “девятки’’).

Сначала докажем, что . В самом деле, каждой последовательности из трех десятичных цифр с суммой цифр от до можно поставить в соответствие последовательность из трех десятичных цифр с суммой цифр следующим образом: каждую цифру в исходной последовательности заменим на цифру . Тем самым, каждой последовательности из трех десятичных цифр с суммой цифр от до будет соответствовать одна и только одна последовательность из трех десятичных цифр с суммой цифр , принимающей значения от до . Значит, таких последовательностей с суммой цифр , где столько же, сколько последовательностей с суммой цифр ().

Далее нам понадобится число способов представления целого неотрицательного числа в виде суммы трех целых неотрицательных слагаемых. Это можно сделать способами. Действительно, число способов равно числу сочетаний с повторениями из по (или иначе, разбиваем единиц на три группы — три слагаемых, в качестве разделителей используем нули, всего элемента, из которых нужно выбрать нуля, см. сочетания с повторениями).

Число способов получить сумму от до можно вычислить по полученной формуле:

: (впрочем, это и так очевидно, , иначе никак),

: ,

: .

Теперь перейдем к . Здесь все немного сложнее, потому что цифры не существует, и нам нужно из всех способов разбиения числа не три целых неотрицательных слагаемых вычесть те способы, в которых одно из слагаемых равно . Подсчитать эти способы можно довольно легко. Мы первое слагаемое в разложении числа на сумму трех слагаемых положим равным , а дальше подсчитаем количество способов представить оставшееся число () в виде суммы трех целых неотрицательных слагаемых (этих способов ). Получаем (с учетом того, что слагаемое может стоять на трех разных местах)

: .

Для поступаем точно так же. Сначала находим число способов представить в виде суммы трех целых неотрицательных слагаемых — оно равно , а затем вычитаем те способы, в которых одно из слагаемых больше либо равно десяти — их всего . Итак,

: ,

: .

Число билетов, у которых сумма первых трех цифр равна сумме последних трех цифр и равна , находится как (независимо от способа выбора первых трех цифр с суммой мы можем выбрать три последние цифры, сумма которых также равна ).

Осталось найти общую сумму:

Итак, всего есть “счастливых’’ билета.

hijos.ru

Математика удачи: Ищем счастливые билеты

Чтобы посчитать точное количество, заменим каждую из трёх последних цифр на дополняющую её до 9. D заменим на K = (9 – D), E на M = (9 – E), F на N = (9 – F). Так как исходно A + B + C = D + E + F, то теперь для числа ABCKMN:

A + B + C + K + M + N

=

A + B + C + 9 – D + 9 –E + 9 – F

=

27

Итак, количество счастливых билетов в точности равно количеству чисел от 000000 до 999999, сумма цифр которых равна 27. Стало немного легче, но предстоит ещё немало работы. Сперва вычислим искомое количество. Для этого нарисуем таблицу, в которой по горизонтали укажем количество используемых цифр, а по вертикали — искомую сумму. Таким образом мы последовательно ответим на все вопросы вида «Сколько существует способов представить число k в виде суммы n цифр». Делать это мы будем рекурсивно, то есть выражать большие значения через меньшие. Поехали!

Очевидно, что в первом столбце у нас будет по одному способу получить числа от 0 до 9 (с помощью одной цифры), а всё, что больше 9, — 0 способов.

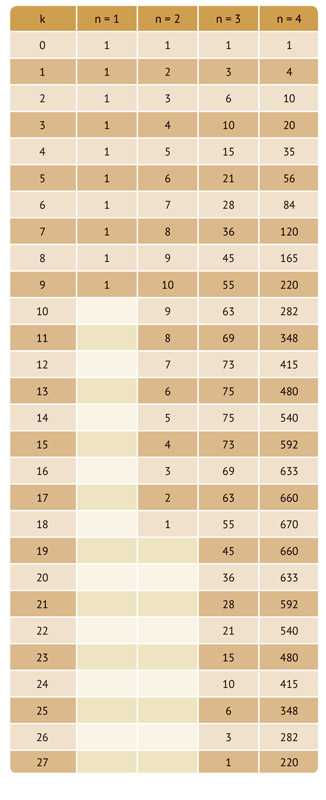
Далее, если перейти ко второму столбцу и взять, допустим, число на пересечении второго столбца и шестой строки (k = 5), сколько существует способов представить 5 в виде суммы двух цифр? Логика тут простая. В качестве второй цифры мы можем выбрать любой из вариантов от 0 до 5. Если выбираем 0, то сумма всех цифр, кроме второй, должна быть равна 5 (да-да, понятно, что в данном случае «всех, кроме второй» — это только первая цифра, но давайте сразу составим алгоритм в общем виде). Если выбираем в качестве второй цифры 1, то сумма оставшихся должна быть равна 4 и т. д. Но ведь тогда мы просто должны сложить способы из предыдущего столбца — для всех чисел от 0 до 5! И получить 6 вариантов.

Ещё пример: допустим, я хочу заполнить во втором столбце поле для k = 11. Несложно увидеть, что тогда вторая цифра 0 или 1 не даёт ни одного варианта, так как первая не может быть больше 9. Иначе говоря, мы обращаемся к пустым ячейкам первого столбца, которые соответствуют k = 10 и k = 11. Впрочем, можно считать, что там не пустота, а нули — это не важно. Так или иначе, мы должны сложить все варианты из предыдущего столбца, от k = 2 до k = 11. Это даёт 8. Таким же образом заполняем второй столбец. Последнее число мы впишем при k = 18, так как максимальная сумма двух цифр равна 18.

Переходим к третьему столбцу. Давайте ещё раз посмотрим на примере, как он заполняется. Допустим, k = 15. Тогда, поскольку последняя цифра может быть от 0 до 9, сумма первых двух должна быть равна 6, 7, 8, 9, …, 15. А для всех этих чисел мы уже знаем количество способов представить их в виде суммы двух цифр. Берём эти значения из таблички (это числа 7, 8, 9, 10, 9, 8, 7, 6, 5 и 4), складываем их и получаем результат: 73 способа представить 15 в виде суммы трёх цифр.

Действуя аналогично, продолжаем заполнять табличку. Занятие это весьма муторное, но конечное. Особенно если написать программу. Но можно сделать всё и руками — главное, нигде не обсчитаться. И если довести таблицу до шестого столбца, число, соответствующее k = 27, и будет искомым ответом. Если вы не ошибётесь, то получите ровно 55 252.

oyla.xyz

Счастливые билетики / Блог им. unC0Rr / OpenLife

Про счастливые билеты написано довольно много: оценка количества таких билетов, общая формула для n-значных билетов в m-ичной системе счисления, московская и ленинградская системы определения «счастливости», график распределения счастливых билетов. Как стартовую точку по этой теме, рекомендую статью на Википедии.

Тем не менее, счастливые билеты хранят в себе некоторые пока неисследованные тайны, о которых я расскажу.

Речь пойдёт о распределении счастливых билетов. Количество шестизначных счастливых билетов равняется 55252, следовательно, вероятность получить такой билет равняется 0,055252. Но какова вероятность получить счастливый билет в случае, когда вы едете не один, и покупаете сразу несколько билетов? Теория вероятностей не помогает ответить на этот вопрос, поскольку речь идёт о нескольких билетах подряд, а не о случайной выборке билетов.

Для исследования вопроса воспользуемся программой на языке Haskell, которая рассчитает интересующие нас данные методом перебора, и рассмотрим случаи московской и ленинградской систем на шестизначных билетиках.

Определим множество всех билетов:

> bilets = [0..999999]

и функции определения счастливости по московской и ленинградской системе:

> -- сумма цифр на чётных позициях равна сумме цифр на нечётных
> isLuckyL a = 
>     ((a `mod` 10) + ((a `div` 100) `mod` 10) + ((a `div` 10000) `mod` 10)) 
>     == (((a `div` 10) `mod` 10) + ((a `div` 1000) `mod` 10) + ((a `div` 100000) `mod` 10)) 

> -- сумма первых трёх цифр равна сумме последних трёх
> isLuckyM a = 
>     ((a `mod` 10) + ((a `div` 10) `mod` 10) + ((a `div` 100) `mod` 10)) 
>     == (((a `div` 1000) `mod` 10) + ((a `div` 10000) `mod` 10) + ((a `div` 100000) `mod` 10))

Нам нужно определить для каждой последовательности из нескольких билетов подряд, есть ли в ней хотя бы один счастливый. Для этого определим список distances, который будет хранить в себе расстояние от билетика до следующего счастливого.

> distances = map distance tickets
>    where
>    distance ticket = if isLuckyL ticket then 0 else 1 + distance (ticket + 1)

Теперь легко узнать, сколько существует групп из n последовательных билетов, среди которых есть хотя бы один счастливый, применив фильтрацию по расстоянию.

 > counts a = show a ++ ": " ++ show (length $ filter (a > ) distances)

Выведем количество таких последовательностей для всех последовательностей длиной от 1 до 1000.

> main = putStrLn $ unlines $ map counts [1..1000]

Применяя в функции distances isLuckyL или isLuckyM, получим данные для ленинградской или московской систем соответственно.

Теперь самое интересное — анализ данных. Построим график зависимости количества счастливых последовательностей билетиков от их длин:

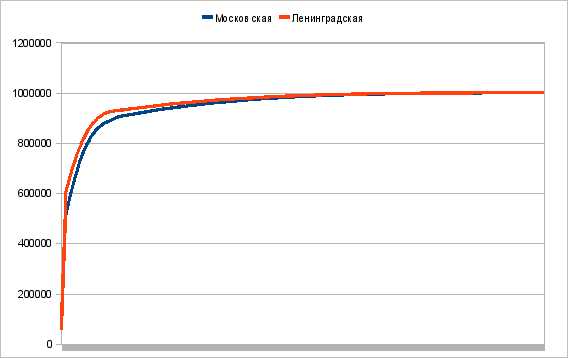
Из графика видно, что ленинградская система на некотором промежутке длин даёт большую вероятность получить счастливый билетик, чем московская. По данным программы, при длинах от 1 до 10 вероятности в обеих системах равны, а при больших длинах ленинградская система выгоднее московской. Так, при 11 билетиках подряд шанс получить счастливый билет по московской системе 506269 из миллиона, по ленинградской — 552511 из миллиона, то есть на 4,6% выше.

Из полученных данных следует, что при езде вдесятером у вас есть неплохие шансы на счастливый билет (49,7%), если конечно, он достанется именно вам. Также, при езде большими группами выгоднее придерживаться ленинградской системы.

P.S. Текст заметки является программой на Literate Haskell.

open-life.org

Счастливый билет — это… Что такое Счастливый билет?

Счастли́вый биле́т — поверье и математическое развлечение, основанное на нумерологической игре с номером проездного билета. Счастливым считается полученный в общественном транспорте билет, в шестизначном номере которого сумма первых трёх цифр совпадает с суммой трёх последних. Общее число шестизначных номеров, порождающих счастливые билеты, равно 55251 (55252, если учитывать билет с номером 000000^[1]), то есть в среднем примерно один билет из восемнадцати является счастливым.

Игры с использованием счастливых билетов часто применяются в школе для обучения детей арифметике. Однако со счастливыми билетами связаны и более серьёзные математические задачи, поскольку последовательные номера билетов представляют собой числовую последовательность.

Счастливые билеты бывают объектом коллекционирования, поскольку сохранение билета считается необходимым условием для того, чтобы он выполнил свою функцию — принёс удачу. Другой путь привлечь удачу с помощью такого билета — это его съесть (как съедают, например, пятилепестковый цветок сирени).

Счастливый билет номер 268736
Счастливые билеты в Новосибирске, Мурманске и Краснодаре

Региональные особенности

«Счастливость» билета можно определить несколькими методами. Наибольшее распространение получили три из них:

Московский — если на автобусном билете напечатано шестизначное число, и сумма первых трёх цифр равна сумме последних трёх, то этот билет считается счастливым.
Ленинградский, или Питерский (менее распространённый) — если сумма чётных цифр билета равна сумме нечётных цифр билета, то билет считается счастливым (в статье журнала «Квант» именно этот способ назван «московским»). Другой вариант — суммы каждой пары цифр равны.
Некоторые люди считают билет счастливым, если сумма его цифр является квадратом. Количество таких билетов с шестизначными номерами равно 99153.

Явные формулы

Точное количество счастливых билетов, определяемых как равенство сумм заданных трёх цифр сумме трёх остальных (Московская и Ленинградская системы) можно посчитать по формуле:^[2]^[3]

которая является частным случаем более общей формулы для нахождения количества 2n-значных счастливых билетов в m-ричной системе счисления (в обычных счастливых билетах используется десятичная система счисления с m=10):

Распределение билетов

В московском и ленинградском методах в среднем один из восемнадцати билетов является счастливым. Однако билеты распределены неравномерно, и вероятность встретить счастливый билет сильно зависит от первых его цифр.

Ниже представлено количество счастливых билетов в каждой тысяче.

Значения цветов

Московский способ

Ленинградский способ

Интересные факты

Примечания

См. также

Ссылки

dic.academic.ru

Счастливый билет — Википедия

Счастли́вый биле́т — поверье и математическое развлечение, основанное на нумерологической игре с номером проездного билета.

Счастливым считается полученный в общественном транспорте билет, в шестизначном номере которого сумма первых трёх цифр совпадает с суммой трёх последних. Общее число шестизначных номеров, порождающих счастливые билеты, равно 55251 (55252, если учитывать билет с номером 000000^[1]), то есть в среднем примерно один билет из восемнадцати является счастливым. Также существует определение «счастливости», согласно которому совпадать должны не сами суммы, а их числовые корни (или, эквивалентно, остатки при делении на 9) — в таком случае счастливых билетов больше.

Региональные особенности[править]

Московский — если на автобусном билете напечатано шестизначное число, и сумма первых трёх цифр равна сумме последних трёх, то этот билет считается счастливым.
Ленинградский, или Питерский (менее распространённый) — если сумма цифр, стоящих на чётных местах билета, равна сумме цифр, стоящих на нечётных местах билета, то билет считается счастливым (в Санкт-Петербурге, напротив, именно этот способ называют «московским»). Другой вариант — суммы каждой пары цифр равны.
В журнале «Квант» от июля 1975 ^[2] года указано, что метод подсчета суммы первых и вторых троек чисел москвичи называют московскими, а ленинградцы — ленинградским, соответственно метод подсчета сумм четных и нечетных позиций приписывают другому городу.
Некоторые люди считают билет счастливым, если сумма его цифр является квадратом. Количество таких билетов с шестизначными номерами равно 99153.

Распределение билетов[править]