Закон сохранения энергии кратко: Закон сохранения энергии, общая форма. Полная энергия: механическая, кинетическая, потенциальная. Формулировка, формулы

Закон сохранения энергии, общая форма. Полная энергия: механическая, кинетическая, потенциальная. Формулировка, формулы

Тестирование онлайн

Закон сохранения энергии

Полная механическая энергия замкнутой системы тел остается неизменной

Закон сохранения энергии можно представить в виде

Если между телами действуют силы трения, то закон сохранения энергии видоизменяется. Изменение полной механической энергии равно работе сил трения

Рассмотрим свободное падение тела с некоторой высоты h2. Тело еще не движется (допустим, мы его держим), скорость равна нулю, кинетическая энергия равна нулю. Потенциальная энергия максимальная, так как сейчас тело находится выше всего от земли, чем в состоянии 2 или 3.

В состоянии 2 тело обладает кинетической энергией (так как уже развило скорость), но при этом потенциальная энергия уменьшилась, так как h3 меньше h2. Часть потенциальной энергии перешло в кинетическую.

Состояние 3 — это состояние перед самой остановкой. Тело как бы только-только дотронулось до земли, при этом скорость максимальная. Тело обладает максимальной кинетической энергией. Потенциальная энергия равна нулю (тело находится на земле).

Полные механические энергии равны между собой , если пренебрегать силой сопротивления воздуха. Например, максимальная потенциальная энергия в состоянии 1 равна максимальной кинетической энергии в состоянии 3.

А куда потом исчезает кинетическая энергия? Исчезает бесследно? Опыт показывает, что механическое движение никогда не исчезает бесследно и никогда оно не возникает само собой. Во время торможения тела произошло нагревание поверхностей. В результате действия сил трения кинетическая энергия не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.

При любых физических взаимодействиях энергия не возникает и не исчезает, а только превращается из одной формы в другую.

Главное запомнить

1) Суть закона сохранения энергии

Урок 23.

наиболее общие законы природы. законы сохранения — Естествознание — 10 класс

Естествознание, 10 класс

Урок 23. Наиболее общие законы природы. Законы сохранения

Перечень вопросов, рассматриваемых в теме:

• В чем смысл закона сохранения энергии;
• Какие виды энергии существуют;
• В чем смысл закона сохранения импульса;
• Что такое момент импульса;
• Как проявляется закон сохранения момента импульса.

Глоссарий по теме:

Энергия (от др.-греч. ἐνέργεια — действие, деятельность, сила, мощь) – это универсальная мера различных форм движения и взаимодействия. Энергия — это характеристика состояния тела или системы тел, зависящие от параметров состояния, её изменение определяется работой.

Работа – физическая величина, характеризующая количество энергии, переданной или полученной системой путём изменения её внешних параметров.

Кинетическая энергия — характеризует движение тела.

Это векторная физическая величина. Она равна нулю, когда тело неподвижно.

Потенциальная энергия – это энергия, обусловленная взаимным расположением тел и характером их взаимодействия. потенциальная энергия всегда характеризует тело относительно источника силы (силового поля). Например, потенциальная энергия гравитационного поля, электромагнитного поля, упругая деформация и др.

Внутренняя энергия — энергия, зависящая от его внутреннего состояния. Включает кинетическую энергию теплового движения микрочастиц (ядер, атомов, молекул, ионов и т.д.) и энергию их взаимодействия. Внутренняя энергия зависит от массы тел, от температуры тел, а также от того, в каком агрегатном состоянии они находятся. Внутренняя энергия тела изменится, если его деформировать или размельчить. Однако она не зависит от того, обладает тело механической энергией или нет.

Замкнутая система – идеализированная модель системы тел, для которой равнодействующая внешних сил равна нулю.

Например, Замкнутая система в механике может быть определена как такая система тел, на которую не действуют внешние силы, либо действия этих внешних сил на тела системы полностью скомпенсированы.

Закон сохранения энергии — фундаментальный закон природы, в замкнутой системе тел полная энергия не изменяется при любых взаимодействиях внутри этой системы тел. Закон накладывает ограничения на протекание процессов в природе. Природа не допускает появление энергии ниоткуда и исчезание в никуда.

Импульс – векторная величина, равная произведению массы тела на скорость его движения, иногда называется количеством движения.

Закон сохранения импульса — для замкнутой системы внешние силы отсутствуют и таким образом импульс замкнутой системы сохраняется, т.е. остаётся неизменным со временем.

Закон сохранения момента импульса

: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени; или импульс системы материальных точек сохраняется, если система замкнута или если сумма моментов всех внешних сил, действующих на систему, равна нулю.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

Естествознание. 10 класс [Текст]: учебник для общеобразоват. организаций: базовый уровень / И.Ю. Алексашина, К.В. Галактионов, И.С. Дмитриев, А.В. Ляпцев и др. / под ред. И.Ю. Алексашиной. – 3-е изд., испр. – М.: Просвещение, 2017.: с 112 — 114.

Электронные ресурсы:

Крис Вудфорд «Атомы у нас дома». Глава из книги// электронный доступ: https://elementy.ru/bookclub/chapters/433839/Atomy_u_nas_doma_Glava_iz_knigi

Альберт Эйнштейн, Леопольд Инфельд «Эволюция физики. Развитие идей от первоначальных понятий до теории относительности и квантов» // электронный доступ: https://elementy.ru/bookclub/chapters/430770/III_Pole_i_otnositelnost

Теоретический материал для самостоятельного изучения

Анализ закономерностей природы позволил выделить Всеобщие законы, которые проявляются на всех уровнях её организации. Эти законы оказываются справедливыми для всех явлений и процессов. Они не зависят не только от людей, но и от систем отсчёта (т.е. они инвариантны), что означает их объективность. Поиск законов – это поиск наиболее объективного, наиболее соответствующего природе способа выражения знаний человека о мире.

К наиболее общим законам природы относят законы сохранения.

Закон сохранения энергии.

Понятие энергии встречается во всех естественных науках.

Энергия – это универсальная мера различных форм движения и взаимодействия. Энергия — это характеристика состояния тела или системы тел, зависящая от параметров состояния, её изменение определяется работой.

Открытие закона сохранения энергии приводят все знания о природе в единую систему. Все наши знания, представления о физических, химических, биологических и др. процессах. Универсальность этого закона позволяет объединить различные виды энергии (механическую, электромагнитную, тепловую и т.д.).

Суть закона сохранения энергии состоит в том, что энергия любого вида может передаваться от одного тела другому или превращаться из одного вида энергии в другой, притом так, что в процессах передачи и превращения энергия бесследно не исчезает и не возникает из ничего.

Если мы представим себе систему, которая не взаимодействует с окружающей средой, т.е. не получает энергии извне и не отдаёт свою энергию, то можно говорить, что энергия этой замкнутой системы останется неизменной. В природе отсутствуют системы, которые совершенно не взаимодействуют с окружающей средой — природные системы являются открытыми. Однако любая природная система является частью системы более высокого уровня. Поэтому закон сохранения энергии оказывается справедлив и в этом случае.

Закон сохранения механической энергии — частный случай фундаментального закона сохранения энергии:

E_м = E_p + E_k = const

При этом различают кинетическую и потенциальную энергии. Они могут переходить друг в друга. Примером может служить движение маятника. Механическая энергия является суммой этих двух видов энергий. Не сложно предположить, что если маятник оказался бы замкнутой системой, его движение было бы бесконечно. Однако взаимодействуя с окружающей средой, часть энергии переходит во внутреннюю энергию. Так, если присутствуют силы трения или произойдёт неупругий удар, тела могут нагреваться, т.е. механическая энергия переходит в тепло (внутреннюю энергию движения частиц). Внутренняя энергия также может переходить в механическую, что происходит, например, при движении живых организмов и при работе тепловых двигателей.

Помимо тепловой, электрическая, химическая и ядерная энергии — это виды внутренней энергии, которые вносят вклад в общее содержание энергии в веществе. Так в лампе накаливания можно наблюдать переход электрической энергии в тепловую. Электродвигатель преобразует энергию электромагнитного поля в механическую. Энергия химических связей может высвобождаться в форме тепловой энергии, например при горении. Энергия ядра в атомных реакторах преобразуется в тепловую.

На фундаментальном уровне, таким образом, любую энергию можно в итоге свести к кинетической энергии частиц вещества и энергии фундаментальных полей.

Напомним, что обмен энергией с окружающей средой является одним из необходимых условий существования всего живого.

Закон сохранения импульса

Помимо энергии есть ещё одна характеристика вещества и поля – импульс. Впервые этим термином описал движение Рене Декарт. Импульс он определил как количество движения. Действительно, не всегда описание движения скоростью, ускорением и т.п. удобно. Так, например, при торможении поезда и велосипеда, двигающихся с одинаковой скоростью, тормозной путь будет больше. Согласитесь, что только скоростью это объяснить нельзя. Здесь важно учитывать и массу.

Величина равная произведению массы и скорости тела называется импульсом:

Это величина векторная. И её вектор направлен в том же направлении что и скорость.

Введение импульса действительно оправдано. Ведь он у тела никуда не девается, импульс сохраняется. Иллюстрацию этого можно наблюдать на примере маятника, называемого колыбелью Ньютона.

Согласно закону сохранения импульса, импульс замкнутой системы остаётся неизменным (p = const). Он может измениться только при действии внешних сил.

Импульс всегда связан со взаимодействием. Так внутренняя энергия не может изменить импульс системы. Т.е. вытаскивание себя из болота за волосы, как предлагал Мюнхгаузен, дело бесперспективное.

С другой стороны, тогда бы и ракета не смогла бы двигаться в безвоздушном пространстве космоса, попросту не от чего «оттолкнуться». В этом случае важно учитывать векторную сумму импульсов тел нашей замкнутой системы. Если появляется импульс, то тело начнёт своё движение, чтобы скомпенсировать его, при этом в противоположную сторону. Так воздушный шарик с воздухом изначально имеет нулевой импульс. Тогда, согласно закону сохранения импульса, выпуская воздух, система всё равно должна сохранить своё нулевое значение. Воздух, вырываясь с определённой скоростью, компенсируется движением шарика, в противоположном направлении воздушной струи.

Закон сохранения импульса можно наблюдать не только на примере движения животных, таких как кальмар, осьминог и др. Похожее реактивное движение используется и в космических ракетах. Разогретый газ, вырывающийся из сопел, является «опорой», для ракеты.

Заметим, что фундаментальные поля тоже характеризуются импульсом и при взаимодействии с веществом могут приводить его в движение

Закон сохранения момента импульса

При вращательном движении аналогом импульса тела поступательного движения, будет выступать момент импульса тела относительно оси. Эта величина зависит от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Ярким примером закона сохранения момента импульса является раскрученный волчок (юла). С точки зрения этого закона можно рассматривать вращательное движение планет вокруг Солнца. В этом случае, момент импульса будет высчитываться по формуле:

Не сложно сделать вывод, что поскольку масса, радиус и скорость не меняются, то и момент импульса останется неизменным ().

В случае движения тел по эллиптической орбите, закон сохранения момента импульса останется справедливым. В этом случае момент импульса будет выражаться следующим образом:

α — угол между вектором скорости тела и направлением на Солнце.

Следуя закону сохранения импульса, подлетая к Солнцу, например комета, будет ускоряться, т.к. радиус становится меньше.

Закон сохранения момента импульса наглядно проявляется, в гимнастических упражнениях, спортсмены совершают вращательные движения. Сжимаясь и распрямляясь, спортсмен заметно изменяет скорость своего вращения.

Момент импульса системы тел определяется как сумма моментов импульса каждого из тел.

Этот закон справедлив и в микромире, При этом важно отметить, что все частицы обладают моментом импульса, что свидетельствует о том, что им свойственно и движение «вокруг своей оси». Эту характеристику частиц обозначают спином.

Закон сохранения момента импульса справедлив не только для замкнутых систем, но равноправен и в тех случаях, когда внешние силы направлены к центру. Например, попробуйте остановить колесо велосипеда, действуя только на ось его вращения.

Вывод:

Законы сохранения импульса, момента импульса, энергии отражают общий принцип сохранения материи и движения, служат доказательством существования всеобщих взаимосвязей в природе. Объективность законов природы, их общность приводит к выводу о единстве законов природы, что подтверждает единство природы в целом.

Примеры и разбор решения заданий тренировочного модуля:

Задание 1.

Выберите один ответ:

Что произойдёт, если дети на раскрученной карусели одновременно переместятся ближе к центру?

Скорость вращения карусели увеличится;

Скорость вращения карусели уменьшится;

Скорость вращения карусели останется неизменной;

Ответ: Скорость вращения карусели увеличится

Пояснение: В соответствии с законом сохранения, момент импульса замкнутой системы останется неизменным L=const. Поскольку момент импульса связан с массой, скоростью и радиусом (L= m∙v∙r), то несложно оценить, что при неизменной массе, но при уменьшающемся радиусе, величина скорости увеличивается, что мы и можем наблюдать в примере

Задание 2.

Почему в действительности Мюнхгаузен не мог вытащить за волосы себя из болота?

А) Плечо силы было бы недостаточно;

Б) Момент сохранения момента импульса применим только для замкнутых систем, каковой человек не является;

В) Для изменения импульса замкнутой системы необходимо, чтобы произошло взаимодействие с другим телом, т.е. «нужно от чего-нибудь оттолкнуться»;

Ответ: В.

Пояснение: Импульс всегда связан с взаимодействием. Внутренняя энергия не может изменить импульс системы. Т.е. вытаскивание себя из болота за волосы, как предлагал Мюнхгаузен, дело бесперспективное.

1. Закон сохранения энергии — Физика это просто!!! 2016

 

Фундаментальный закон природы, установленный эмпирически (т.е. в опытах) и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется неизменной с течением времени.

Выше мы уже писали: все, что мы знаем про энергию, это что есть такая скалярная величина, которая в замкнутой системе остается всегда постоянной.

На самом деле это очень круто! Благодаря энергии мы можем сравнивать и изучать взаимодействие различных явлений — механических, электромагнитных, тепловых и пр.

Так как этот закон относится не к конкретным физическим величинам (скорость, температура, импульс, и т.п.), а показывает общую закономерность всех явлений в природе (везде и всегда безо всякий исключений!), то иногда его называют принципом сохранения энергии, выделяя таким образом среди всех физических законов сохранения.

В ньютоновской механике формулируется частный случай общего принципа сохранения энергии — Закон сохранения механической энергии: «Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.»

В школьной программе по физике силы разделяют на консервативные и неконсервативные(диссипативные) силы. Консервативные силы (потенциальные силы) — это силы, работа которых не зависит от вида траектории.

Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия.

Примером неконсервативной силы является сила трения.

Сохранение энергии означает, что при отсутствии в замкнутой механической системе диссипативных сил (например, сил трения) механическая энергия не может возникнуть из ничего и не может исчезнуть в никуда.

      На рисунке приведен пример замкнутой механической системы – груз массой m совершает колебания под действием силы упругости пружины жесткостью k. Трением в системе пренебрегаем, т.е. считаем силы трения равными 0.

В крайних положениях с максимальным отклонением X потенциальная энергия максимальна, кинетическая в системе координат с началом в точке равновесия, например, равна 0 (подходит любая инерциальная система координат, покоящаяся относительно точки равновесия данного маятника).

В момент прохождения грузом точки равновесия наоборот. Кинетическая энергия максимальна, а потенциальная энергия равна 0.

Запишем это в виде уравнений (помним, что у нас одномерный случай):

В одномерном случае вместо векторов можно рассматривать просто значения одной компоненты (по оси X в данном случае). Мы помним из задачи про круговое движение, что составляющая ускорения по оси X при равномерном круговом движении с центром окружности в начале координат равна:

       Можно сказать, что координата x совершает гармонические колебания с циклической частотой . Выше мы эту величину назвали угловой скоростью, измеряемой в радианах в секунду. И она была связана с периодом обращения точки по окружности:

        Этот период равен периоду колебания координаты x (и, кстати, равен также периоду колебания координаты y) при движении по окружности с постоянной угловой скоростью. Поэтому в случае описания гармонических колебаний величина ω —  называется циклической частотой. В случае с колебаниями нашего грузика на пружине:

     Эта формула называется формулой Гюйгенса.

         Мы помним (а если еще не помним, то запоминаем!), что потенциальная энергия упруго деформированного тела равна

             Почему? А вот почему. Потенциальная энергия – это величина, изменение которой характеризует работу, произведенную силой, которая является причиной этой потенциальной энергии. Они обе, и энергия и работа измеряются в одних и тех же единицах – Джоулях. Тогда, при малом смещении Δx

Причем Δx – это такое маленькое смещение под действием силы F_упр, что мы можем считать эту силу постоянной в пределах величины этого смещения.  Тогда ∆A(x) – это работа произведенная нашей силой упругости на отрезке Δx.

Заметили, что x и Δx в нашем случае разных знаков? Догадайтесь почему!

И не забывайте, что мы взяли отрезок Δx настолько маленьким, что силу F_упр(x) можно считать на нем постоянной. Это вообще то правильно только если смещение Δx бесконечно малое — dx. Обозначим  dA(x) величину работы на бесконечно малом отрезке dx.

            Выберем начало координат в точке равновесия. Там  x = 0

            Тогда работа при бесконечно малом смещении от точки x буде равна

            Теперь суммируем все «кусочки работ» dA на отрезках dx от X до 0. Так как они (отрезки dx) бесконечно маленькие, то такое суммирование бесконечного числа бесконечно малых отрезков на которые поделен конечный отрезок есть, как мы помним, операция интегрирования.

            Понятно, почему у интеграла внизу стоит X, а вверху 0?

            Потому что мы суммируем от координаты X к координате 0! Мы в самом начале оговорили, что рассматриваем работу, которую совершает сила упругости. Соответственно, у нас движение идет по направлению силы упругости. Логично, что потенциальная энергия в процессе совершении такой работы уменьшается. Так как сокращается расстояние до точки равновесия с одной стороны, и уменьшается сила с другой. Сильно растянутая (или сжатая пружина) прилагает к грузику большую силу, чем слабо растянутая. Значит, когда мы растягиваем (или сжимаем) пружину против ее усилий, мы увеличиваем ее потенциальную способность совершить работу. А когда он сжимается или растягивается под влиянием своей собственной силы упругости, тогда ее потенциальную способность совершать работу уменьшается.

            Проинтегрировав, мы найдем полную работу, которую совершит пружина, пройдя расстояние от максимального отклонения от точки равновесия X до точки равновесия, где по нашему определению потенциальная энергия пружины равна нулю. Эта работа равна разнице значений первообразных функции (-k*x) (первообразную можно посмотреть в таблице или найти в интернете)в точке 0 (верхняя граница интегрирования) и X (нижняя граница интегрирования:

            Итак, потенциальную энергию пружины в любой произвольно выбранной точке X мы нашли. А что же с кинетической энергией?

            Найдем для начала кинетическую энергию в точке равновесия пружины с координатой x = 0. По Закону сохранения энергии кинетическая энергия в точке равновесия пружины равна потенциальной энергии в точке максимального отклонения пружины от точки равновесия. Снова посмотрим на на рисунок!

            Следовательно, полная энергия пружины с грузиком в произвольной точке с координатой отклонения x равна:

            Так как у нас в формуле стоят квадраты, то на знаки координаты и скорости можно не обращать внимания. Хотя неплохо бы представлять себе, когда и каких они знаков. Заметим, также, что эта формула позволяет нам находить скорость грузика на пружине в любой точке, если заданы жесткость пружины, масса грузика и полная энергия системы (или максимальное отклонение).

            Ну а теперь не откажем себе в удовольствии еще раз вывести формулу для ускорения грузика на пружине в произвольной точке x.

            Продифференцируем уравнение полной энергии системы по времени t. Это можно сделать, так как у нас координата x = x(t) зависит от времени t. Помним, что E_полн = const:

      Смотрим в раздел про производные функций или открываем http://www.wolframalpha.com/.Дифференцируем:

            Так как скорость v(t) не всегда равна нулю, то нулю равно выражение в скобках. Из чего мы получаем туже самую формулу, только полученную непосредственно из закона сохранения энергии:

Чтобы закрепить понятие сохранения энергии в замкнутой механической системе, рассмотрим еще одну классическую задачу. Задачу про движение тел под действием силы тяжести.

            Когда какое-либо маленькое и тяжелое (но не сверхтяжелое!) тело падает вблизи поверхности Земли, можно с достаточной точностью считать, что на тело действует постоянная по величине сила тяжести, сообщающая телу ускорение g, приблизительно равное 9,8 м/с².

            Почему маленькое и тяжелое? Чтобы можно было пренебречь сопротивлением воздуха. А почему не сверхтяжелое?

            Правильно! Чтобы можно было пренебречь влиянием самого тела на Землю. Потому, что вообще то тело тоже притягивает Землю. И хотя значение ускорения, которое испытывает тело, не изменяется в зависимости от его массы. Да, да! Солнце тоже испытывало бы ускорение g. если бы центр массы Солнца находился бы на уровне поверхности Земли. Закон тяготения никто не отменял!

То есть ускорение, придаваемое Землей телу, которое притягивает Земля, не зависит от массы этого тела, а зависит только от массы земли и расстояния от центра тяжести (центра масс) Земли до центра масс притягиваемого тела.

Теперь пора рассмотреть задачу о падающем камне. Например, такую:

1)     «Если тело свободно отпустить с высоты 40 м, его скорость в момент падения на Землю составит…      Ответ: ___ м/с.»

Или такую:

2)     «Тело подбрасывают вверх со скоростью 10 м/с с высоты 50 метров над поверхностью Земли. Какая скорость будет у тела на высоте 30 метров над поверхностью Земли?»

Начнем с первой. Все подобные задачи решаются, исходя из знания Закона сохранения энергии. Первое, мы понимаем, что система «тело-Земля» замкнутая. Второе, в этой системе существует только сила притяжения и никаких других сил, типа диссипативной (неконсервативной) силы трения тела о воздух. И еще оно относительно Земли легкое, настолько, что не ускоряет саму Землю. Правильнее сказать, ускоряет, но пренебрежимо мало. И еще, что наше тело относительно Земли очень маленькое, так, что его линейными размерами в данной задаче можно пренебречь.

Таким образом, у нас получилась задача о движении тела в поле постоянной силы притяжения в любой точке(F_тяж = const).

Соответственно, полная энергия в момент отпускания равна:

Проверим по формулам равноускоренного движения:

        Правильно!

Заметьте, можно решать и так, и так. Но, с помощью закона сохранения энергии обычно решение получается проще и короче. Покажем это на примере решения второй задачи. Повторим условия: ««Тело подбрасывают вверх со скоростью 10 м/с с высоты 50 метров над поверхностью Земли. Какая скорость будет у тела на высоте 30 метров над поверхностью Земли?».

       Здесь тело сначала двигалось вверх, а затем падало вниз. Соответственно, чтобы решить задачу через уравнения равноускоренного движения, нам нужно сначала найти высоту верхней точки, а для этого нужно определить время подъема. Время подъема – это время до того момента, когда скорость тела будет равна нулю. Затем вычислить высоту подъема. И уже затем решать в точность как первую задачу – в два действия.

       Если решать через закон сохранения энергии, то сначала находим полную энергию на высоте старта, а затем, уже зная полную энергию на высоте 30 метров вычисляем скорость из уравнения с одним переменным:

В конце концов, каждый решает сам, каким способом ему проще решать конкретную задачу. Стоит только иметь ввиду, что есть целая группа задач, самым простым решением которых есть решение через закон сохранения энергии.

       Заметим еще, что как бы мы ни кидали тело, в любом случае на одинаковой высоте в отсутствии диссипативных сил в системе (например, силы трения) скорость тела по модулю будет одинаковой на подъеме и на спуске. Догадайтесь сами, почему!

Потому, что скорость у нас в этой задаче зависит только от высоты

!!!        Мы рассмотрели примеры применения закона сохранения энергии в механике. Но закон справедлив для всех остальных видов энергии (тепловой, электрической и пр.). Вообще всегда! Это очень удобно для описания сложных физических явлений, в которых один вид энергии переходит в другой. Например, при описании паровых машин или двигателей внутреннего сгорания.

 

Закон сохранения энергии.

Титульная Механика Литература

Силы, работа которых не зависит от формы траектории, а определяется начальным и конечным положением тела, называются потенциальными. Очевидно, что работа потенциальных сил на замкнутой траектории равна нулю. Все силы, работа которых зависит от формы траектории, называются непотенциальными. Непотенциальными силами являются силы трения, сопротивления. Для системы тел, в которой действуют потенциальные силы взаимодействия, можно ввести понятие потенциальной энергии. Потенциальная энергия — некоторая функция, описывающая взаимное расположение тел в системе, изменение которой взятое с обратным знаком, равно работе потенциальных сил, действующих между телами ситемы или же это энергия взаимного действия, взаимного расположения тел относительно друг друга: Пример. При прыжке ныряльщика в воду потенциальная сила притяжения совершает работу, которая равна изменению потенциальной энергии ныряльщика. Эта работа идет на изменение кинетической энергии прыгуна. Свойства потенциальной энергии: это энергия системы тел, между которыми действуют потенциальные силы взаимодействия; потенциальная энергия определяется с точностью до постоянного слагаемого. При этом за нулевой уровень потенциальной энергии можно принять любое состояние системы; формула для расчета потенциальной энергии может быть разной и зависит от характера взаимодействия тел; общим для всех видов потенциальной энергии является ее связь с работой потенциальных сил: A=Epсил=-(Ep1-Ep2) Кинетическая энергия — энергия движения. Работа силы, приложенной к телу при изменении его V, равна изменению кинетической энергии: Закон сохранения энергии. Приращение потенциальной энергии брошенного вверх тела происходит за счет убыли его кинетической энергии; при падении тела, приращение кинетической энергии происходит за счет убыли потенциальной энергии, так что полная механическая энергия тела не меняется. Аналогично, если на тело действует сжатая пружина, то она может сообщить телу некоторую скорость, т. е. кинетическую энергию, но при этом пружина будет распрямляться, и ее потенциальная энергия будет соответственно уменьшаться; сумма потенциальной и кинетической энергий останется постоянной. Если на тело, кроме пружины, действует еще и сила тяжести, то хотя при движении тела энергия каждого вида будет изменяться, но сумма потенциальной энергии тяготения, потенциальной энергии пружины и кинетической энергии тела опять-таки будет оставаться постоянной. Энергия может переходить из одного вида в другой, может переходить от одного тела к другому, но общий запас механической энергии остаётся неизменным. Опыты и теоретические расчеты показывают, что при отсутствии сил трения и при воздействии только сил упругости и тяготения суммарная потенциальная и кинетическая энергия тела или системы тел остается во всех случаях постоянной. В этом и заключается закон сохранения механической энергии. Докажем закон сохранения энергии в следующем опыте. Стальной шарик, упавший с некоторой высоты на стальную или стеклянную плиту и ударившийся об неё, подскакивает почти на ту же высоту, с которой упал. Во время движения шарика происходит целый ряд превращений энергии. При падении потенциальная энергия переходит в кинетическую энергию шарика. Когда шарик прикоснется к плите, и он и плита начинают деформироваться. Если рассмотреть кинетическую энергию, то можно сделать вывод, что она превращается в потенциальную энергию упругой деформации шарика и плиты, причем этот процесс продолжается до тех пор, пока шарик не остановится, т. е. пока вся его кинетическая энергия не перейдёт в потенциальную энергию упругой деформации. Затем под действием сил упругости деформированной плиты шарик приобретает скорость, направленную вверх: энергия упругой деформации плиты и шарика превращается в кинетическую энергию шарика. При дальнейшем движении вверх скорость шарика под действием силы тяжести уменьшается, и кинетическая энергия превращается в потенциальную энергию тяготения. В наивысшей точке шарик обладает снова только потенциальной энергией тяготения. Поскольку можно считать, что шарик поднялся на ту же высоту, с которой он начал падать, потенциальная энергия шарика в начале и в конце описанного процесса одна и та же. Более, того, в любой момент времени при всех превращениях энергии сумма потенциальной энергии тяготения, потенциальной энергии упругой деформации и кинетической энергии все время остается одной и той же. Для процесса превращения потенциальной энергии, обусловленной силой тяжести, в кинетическую и обратно при падении и подъеме шарика это было показано простым расчетом. Можно было бы убедиться, что и при превращении кинетической энергии в потенциальную энергию упругой деформации плиты и шарика и затем при обратном процессе превращения этой энергии в кинетическую энергию отскакивающего шарика сумма потенциальной энергии тяготения, энергии упругой деформации и кинетической энергии также остается неизменной, т. е. закон сохранения механической энергии выполнен. Теперь мы можем объяснить, почему нарушался закон сохранения работы в простой машине, которая деформировалась при передаче работы: дело в том, что работа, затраченная на одном конце машины, частично или полностью затрачивалась на деформацию самой простой машины (рычага, веревки и т.д.), создавая в ней некоторую потенциальную энергию деформации, и лишь остаток работы передавался на другой конец машины. В сумме же переданная работа вместе с энергией деформации оказывается равной затраченной работе. В случае абсолютной жесткости рычага, нерастяжимости веревки и т. д. простая машина не может накопить в себе энергию, и вся работа, произведенная на одном ее конце, полностью передается на другой конец. Силы трения и закон сохранения механической энергии. Присматриваясь к движению шарика, подпрыгивающего на плите, можно обнаружить, что после каждого удара шарик поднимается на несколько меньшую высоту, чем раньше, т. е. полная энергия не остается в точности постоянной, а понемногу убывает; это значит, что закон сохранения энергии в таком виде, как мы его сформулировали, соблюдается в этом случае только приближённо. Причина заключается в том, что в этом опыте возникают силы трения, сопротивление воздуха, в котором движется шарик, и внутреннее трение в самом материале шарика и плиты. Вообще, при наличии трения закон сохранения механической энергии всегда нарушается и полная энергия тел уменьшается. За счет этой убыли энергии и совершается работа против сил трения. Например, при падении тела с большой высоты скорость, вследствие действия возрастающих сил сопротивления среды, вскоре становится постоянной; кинетическая энергия тела перестает меняться, но его потенциальная энергия уменьшается. Работу против силы сопротивления воздуха совершает сила тяжести за счет потенциальной, энергии тела. Хотя при этом и сообщается некоторая кинетическая энергия окружающему воздуху, но она меньше, чем убыль потенциальной энергии тела, и, значит, суммарная механическая энергия убывает. Работа против сил трения может совершаться и за счет кинетической энергии. Например, при движении лодки, которую оттолкнули от берега пруда, потенциальная энергия лодки остается постоянной, но вследствие сопротивления воды уменьшается скорость движения лодки, т. е. ее кинетическая энергия, приращение кинетической энергии воды, наблюдающееся при этом, меньше, чем убыль кинетической энергии лодки. Подобно этому действуют и силы трения между твердыми телами. Например, скорость, которую приобретает груз, соскальзывающий с наклонной плоскости, а, следовательно, и его кинетическая энергия, меньше той, которую он приобрёл бы в отсутствие трения. Можно так подобрать угол наклона плоскости, что груз будет скользить равномерно. При этом его потенциальная энергия будет убывать, а кинетическая — оставаться постоянной, и работа против сил трения будет совершаться за счет потенциальной энергии. В природе все движения (за исключением движений в вакууме, например, движений небесных тел) сопровождаются трением. Поэтому при таких движениях закон сохранения механической энергии нарушается, и это нарушение происходит всегда в одну сторону — в сторону уменьшения полной энергии. Превращение механической энергии во внутреннюю энергию. Особенность сил трения состоит, как мы видели, в том, что работа, совершённая против сил трения, не переходит полностью в кинетическую или потенциальную энергию тел; вследствие этого суммарная механическая энергия тел уменьшается. Однако работа против сил трения не исчезает бесследно. Прежде всего, движение тел при наличия трения ведет к их нагреванию. Мы можем легко обнаружить это, крепко потирая руки или протягивая металлическую полоску между сжимающими ее двумя кусками дерева; полоска даже на ощупь заметно нагревается. Первобытные люди, как известно, добывали огонь быстрым трением сухих кусков дерева друг о друга. Нагревание происходит также при совершении работы против сил внутреннего трения, например, при многократном изгибании проволоки. Нагревание при движении, связанном с преодолением сил трения, часто бывает очень сильным. Например, при торможении поезда тормозные колодки сильно нагреваются. При спуске корабля со стапелей на воду для уменьшения трения стапеля обильно смазываются, и все же нагревание так велико, что смазка дымится, а иногда даже загорается. При движении тел в воздухе с небольшими скоростями, например, при движении брошенного камня, сопротивление воздуха невелико, на преодоление сил трения затрачивается небольшая работа, и камень практически не нагревается. Но быстро летящая пуля разогревается значительно сильнее. При больших скоростях реактивных самолетов приходится уже принимать специальные меры для уменьшения нагревания обшивки самолета. Мелкие метеориты, влетающие с огромными скоростями (десятки километров в секунду) в атмосферу Земли, испытывают такую большую силу сопротивления среды, что полностью сгорают в атмосфере. Нагревание в атмосфере искусственного спутника Земли, возвращающегося на Землю, так велико, что на нем приходится устанавливать специальную тепловую защиту. Кроме нагревания, трущиеся тела могут испытывать и другие изменения. Например, они могут измельчаться, растираться в пыль, может происходить плавление, т. е. переход тел из твердого в жидкое состояние: кусок льда может расплавиться в результате трения о другой кусок льда или о какое-либо иное тело. Итак, если движение тел связано с преодолением сил трения, то оно сопровождается двумя явлениями: сумма кинетической и потенциальной энергий всех участвующих в движении тел уменьшается; происходит изменение состояния тел, в частности может происходить нагревание. Это изменение состояния тел происходит всегда таким образом, что в новом состоянии тела могут производить большую работу, чем в исходном. Так, например, если налить в закрытую с одного конца металлическую трубку немного эфира и, заткнув трубку пробкой, зажать ее между двумя пластинками и привести в быстрое вращение, то эфир испарится и вытолкнет пробку. Значит, в результате работы по преодолению сил трения трубки о пластинки трубка с эфиром пришла в новое состояние, в котором она смогла совершить работу, требующуюся для выталкивания пробки, т. е. работу против сил трения, удерживающих пробку в трубке, и работу, идущую на сообщение пробке кинетической энергии. В исходном состоянии трубка с эфиром не могла совершить эту работу. Таким образом, нагревание тел, равно как и другие изменения, их состояния, сопровождается изменением «запаса» способности этих тел совершать работу. Мы видим, что «запас работоспособности» зависит, помимо положения тел относительно Земли, помимо их деформации и их скорости, еще и от состояния тел. Значит, помимо потенциальной энергии тяготения и упругости и кинетической энергии тело обладает и энергией, зависящей, от его состояния. Будем называть ее внутренней энергией. Внутренняя энергия тела зависит от его температуры, от того, является ли тело твердым, жидким или газообразным, как велика его поверхность, является ли оно сплошным или мелко раздробленным и т. д. В частности, чем температура тела выше, тем больше его внутренняя энергия. Таким образом, хотя при движениях, связанных с преодолением сил трения, механическая энергия систем движущихся тел уменьшается, но зато возрастает их внутренняя энергия. Например, при торможении поезда уменьшение его кинетической энергии сопровождается увеличением внутренней энергии тормозных колодок, бандаж колес, рельсов, окружающего воздуха и т. д. в результат нагревания этих тел. Все сказанное относится также и к тем случаям, когда силы трения возникают внутри тела, например, при разминании куска воска, при неупругом ударе свинцовых шаров, при перегибании куска проволоки. Всеобщий характер закона сохранения энергии. Силы трения занимают особое положение в вопросе о законе сохранения механической энергии. Если сил трения нет, то закон сохранения механической энергии соблюдается: полная механическая энергия системы остается постоянной. Если же действуют силы трения, то энергия уже не остается постоянной, а убывает при движении. Но при этом всегда растет внутренняя энергия. С развитием физики обнаруживались все новые виды энергии: была обнаружена световая энергия, энергия электромагнитных волн, химическая энергия, проявляющаяся при химических реакциях (в качестве примера достаточно указать хотя бы на химическую энергию, запасённую во взрывчатых веществах и превращающуюся в механическую и тепловую энергию при взрыве), наконец, была открыта ядерная энергия. Оказалось, что совершаемая над телом работа равна сумме всех видов энергии тела; работа же, совершаемая некоторым телом над другими телами, равна убыли суммарной энергии данного тела. Для всех видов энергии оказалось, что возможен переход энергии из одного вида в другой, переход энергии от одного тела к другому, но что при всех таких переходах общая энергия всех видов остаётся все время строго постоянной. В этом заключается всеобщность закона сохранения энергии. Хотя общее количество энергии остается постоянным, количество полезной для нас энергии может уменьшаться и в действительности постоянно уменьшается. Переход энергии в другую форму может означать переход ее в бесполезную для нас форму. В механике чаще всего это — нагревание окружающей среды, трущихся поверхностей и т. п. Такие потери не только невыгодны, но и вредно отзываются на самих механизмах; так, во избежание перегревания приходится специально охлаждать трущиеся части механизмов.

Закон сохранения механической энергии

При имеющейся замкнутой механической системе тела взаимодействуют посредством сил тяготения и упругости, тогда их работа равняется изменению потенциальной энергии тел с противоположным знаком:

A=–(Eр2–Eр1).

Следуя из теоремы о кинетической энергии, формула работы примет вид

A=Ek2-Ek1.

Отсюда следует, что

Ek2-Ek1=–(Eр2–Eр1) или Ek1+Ep1=Ek2+Ep2.

Кинетическая и потенциальная энергии

Определение 1

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Данное утверждение выражает закон сохранения энергии в замкнутой системе и в механических процессах, являющийся следствием законов Ньютона.

Определение 2

Сумма E=Ek+Ep— это полная механическая энергия.

Закон сохранения энергии выполняется при взаимодействии сил с потенциальными энергиями в замкнутой системе.

Пример N

Примером применения такого закона служит нахождение минимальной прочности легкой нерастяжимой нити, которая удерживает тесло с массой m, вращая его вертикально относительно плоскости (задачи Гюйгенса). Подробное решение изображено на рисунке 1.20.1.

Рисунок 1.20.1. К задаче Гюйгенса, где F→ принимается за силу натяжения нити в нижней точке траектории.

Запись закона сохранения полной энергии в верхней и нижней точках принимает вид

mv122=mv222+mg2l.

F→ располагается перпендикулярно скорости тела, отсюда следует вывод, что она не совершает работу.

Если скорость вращения минимальная, то натяжение нити верхней точке равняется нулю, значит, центростремительное ускорение может быть сообщено только при помощи силы тяжести. Тогда

mv22l=mg.

Исходя из соотношений, получаем

v1 min2=5gl.

Создание центростремительного ускорения производится силами F→ и mg→ с противоположными направлениями относительно друг друга. Тогда формула запишется:

mv122=F-mg.

Можно сделать вывод, что при минимальной скорости тела в верхней точке натяжение нити будет равняться по модулю значению F=6mg.

Очевидно, что прочность нити обязана превышать значение.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

С помощью закона сохранения энергии посредством формулы можно получить связь между координатами и скоростями тела в двух разных точках траектории, не используя анализ закона движения тела во всех промежуточных точках. Данный закон позволяет заметно упрощать решение задач.

Реальные условия для движущихся тел предполагают действия сил тяготения, упругости, трения и сопротивления данной среды. Работа силы трения зависит от длины пути, поэтому она не является консервативной.

Закон сохранения превращения энергии

Определение 3

Между телами, составляющими замкнутую систему, действуют силы трения, тогда механическая энергия не сохраняется, ее часть переходит во внутреннюю. Любые физические взаимодействия не провоцируют возникновение или исчезновение энергии. Она переходит из одной формы в другую. Данный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.

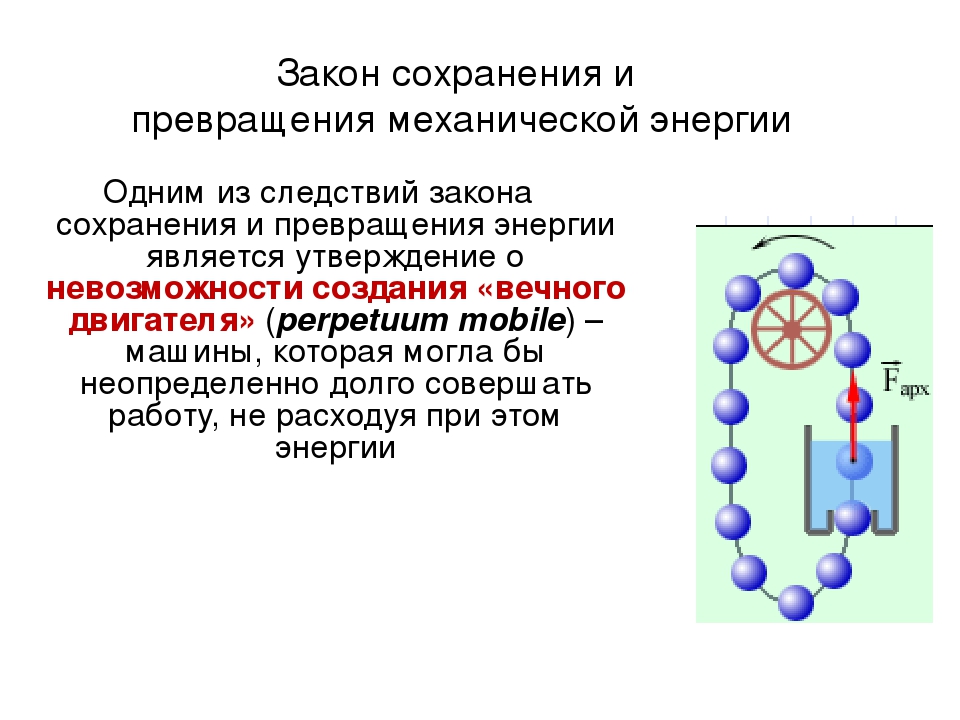
Следствием является утверждение о невозможности создания вечного двигателя (perpetuum mobile) – машины, которая совершала бы работу и не расходовала энергию.

Рисунок 1.20.2. Проект вечного двигателя. Почему данная машина не будет работать?

Существует большое количество таких проектов. Они не имеют право на существование, так как при расчетах отчетливо видны одни ошибки конструкций всего прибора, другие замаскированы. Попытки реализовать такую машину тщетны, так как они противоречат закону сохранения и превращения энергии, поэтому нахождение формулы не даст результатов.

Законы сохранения в механике. Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа.  / / Законы сохранения в механике. Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел Поделиться:    Законы сохранения в механике. Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел Импульс: Второй закон Ньютона в импульсной форме: изменение импульса тела равно импульсу силы: Механическая работа, мощность: Механическая работа постоянной силы F на перемещении s: Работа силы тяжести: Работа силы упругости: Мощность — это работа, совершаемая в единицу времени: Энергия: Энергия — это физическая величина, характеризующая способность тела совершать работу: Кинетическая энергия  — это энергия движущегося тела: Теорема об изменении кинетической энергии:  Изменение кинетической энергии тела за некоторый промежуток времени равно работе, совершенной за это же время силой, действующей на тело: Потенциальная энергия: это энергия взаимодействия тел или частей одного и того же тела: Потенциальная энергия тела на высоте h над землей: Потенциальная энергия упруго деформированного тела: Закон сохранения импульса: Закон сохранения импульса: Независимо от природы сил взаимодействия полный импульс тел, составляющих замкнутую систему, является постоянным: Закон сохранения энергии: Закон сохранения энергии: в замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется: Равновесие твердых тел: Плечо силы d  — это кратчайшее расстояние от оси вращения до прямой, на которой лежит вектор силы F Момент силы F относительно оси вращения:  Первое условие равновесия: Если твердое тело находится в равновесии, то геометрическая сумма внешних сил, приложенных к нему, равна нулю: Второе условие равновесия: При равновесии твердого тела сумма моментов всех внешних сил, приложенных к нему, равна нулю: Поиск в инженерном справочнике DPVA. Введите свой запрос: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

История формулировки закона сохранения энергии

История формулировки закона сохранения энергии

ИСТОРИЯ НАУКИ

В.М.Дуков

Окончание. См. № 24/02

Начало установления количественной связи между работой и теплотой связано с именем молодого французского ученого Сади Карно (1796–1832). Карно – инженер по роду деятельности, физик по складу мышления – племянник замечательного ученого и государственного деятеля периода Великой французской революции Лазара Карно (1753–1823).

В 1814 г. Сади Карно окончил Политехническую школу в Париже, затем поступил в инженерные войска. В 1827 г. он был произведен в капитаны и вскоре вышел в отставку. О его научной деятельности, которую он совмещал с военной службой, известно очень мало. Зато вечную мировую славу завоевала опубликованная в 1824 г. его единственная небольшая книжка «Размышления о движущей силе огня и о машинах, способных развивать эту силу».

В течение 10 лет никто не обращал внимания на эту брошюру, пока ее не «открыл» Клапейрон. Автора уже не было в живых

Интересные записки опубликовал брат Карно после его смерти. В них был, по существу, сформулирован в частной форме закон сохранения энергии. Карно писал в «Размышлениях»: «Тепло – это не что иное, как движущая сила, или, вернее, движение, изменившее свой вид. Это движение частиц тела. Повсюду, где происходит уничтожение движущей силы, возникает одновременно теплота в количестве, точно пропорциональном количеству исчезнувшей движущей силы. Обратно: при исчезновении теплоты всегда возникает движущая сила».

Таким образом, можно высказать общее предположение: движущая сила существует в природе в неизменном количестве; она, собственно, никогда не создается, никогда не уничтожается; в действительности она меняет форму, т.е. вызывает то один род движений, то другой, но никогда не исчезает.

Если «движущую силу» заменить словом «энергия», то перед нами – четкая формулировка закона сохранения энергии. В записках Карно сказано следующее: «По некоторым представлениям, которые у меня сложились относительно теории тепла, создание единицы движущей силы требует затраты 2,7 единицы тепла».

К сожалению, Карно не привел рассуждений, которые привели его к такому результату. Если единицей работы считать кг•м, а единицей теплоты – калорию, то эта оценка близка к полученной далее экспериментаторами.

Но для утверждения связи между работой и теплотой необходим был количественный эксперимент. Нужно было показать, что при затрате единицы работы получается всегда одно и тоже количество теплоты. Это продемонстрировал английский физик Д.П.Джоуль (1818–1889) в своих классических экспериментах, проведенных в 1850 г.

Джоуль родился в Сальфорде близ Манчестера. С ранних лет он проявлял необычайную любознательность и стремление раскрыть тайны природы путем постановки искусного эксперимента. Будучи владельцем большого винного завода (в ученых кругах его называли «пивоваром из Сальфорда»), он завел у себя хорошо оборудованную домашнюю лабораторию, в которой в течение многих лет проводил систематические исследования, направленные на всестороннее обоснование закона сохранения энергии. Его имя увековечено в названии основной единицы энергии.

Схема установки Д.Джоуля

Идейную основу этих довольно сложных в исполнении опытов легко усмотреть из схемы, изображенной на риcунке. Падающие с определенной высоты грузы приводили во вращение вертушку, помещенную в калориметр. Конструкция последнего была такова, что жидкость не могла вращаться всей своей массой, вертушка испытывала сильное сопротивление вращению, и жидкость нагревалась. Зная массу и теплоемкость калориметра, можно по повышению его температуры определить количество выделившейся теплоты: Q = cmDt. Совершенная при этом работа равна потенциальной энергии падающих грузов: А = mgh. Результатом этих опытов, которые затем многократно повторялись в других вариантах, стало знаменитое равенство:

1 Дж = 0,24 кал.

Это так называемый термический эквивалент работы.

Вместо термического эквивалента работы можно говорить о механическом эквиваленте теплоты и результат опытов Джоуля выражать равенством

1 кал = 4,18 Дж.

Заметим, что теплота – специфическая форма движения материи, подчиненная статистическим закономерностям. Энергия теплового движения качественно отлична от механической энергии, что проявляется при превращениях. Механическая энергия целиком переходит в тепловую, равенство 1Дж=0,24кал – результат эксперимента. Но обратный переход – необратимый процесс, – он протекает с потерями, рассеянием энергии, поэтому источник, который отдает количество теплоты, равное 1 кал, производит работу, меньшую 4,18 Дж. Разница переходит во внутреннюю энергию, так что соблюдается закон сохранения энергии

Установление всеобщего закона сохранения энергии и введение интернациональной системы единиц СИ привело к исключению понятия механического эквивалента теплоты. Измерение количества теплоты можно производить в Дж, так что в особой единице для тепловых измерений нет нужды.

3. Осознание общности закона

Начало XIX в. замечательно открытием множества явлений, демонстрировавших превращение сил природы. Первую роль здесь сыграл электрический ток с его химическими, тепловыми, магнитными и электродинамическими действиями. Отсюда умонастроение ученых, которое Фарадей выразил в следующем откровении: «Я давно придерживался мнения, ставшего почти убеждением, что различные формы, в которых проявляются силы материи, имеют общее происхождение или, иными словами, так непосредственно связаны или взаимосвязаны, что они могут превращаться друг в друга и обладают в своих действиях эквивалентами сил».

Убеждение в единстве и взаимной превращаемости сил природы играет роль компаса, ведущего Фарадея в глубь неизведанного. По существу, Фарадей владеет законом сохранения энергии и использует его в качестве инструмента научного исследования.

Вот еще один пример. В «Экспериментальных исследованиях по электричеству» он пишет: «Контактная теория (речь идет о контактной теории гальванической эдс. – В.Д.) принимает, что сила, способная преодолеть мощные сопротивления, может возникнуть из ничего. Это было бы сотворением силы, что нигде не имеет места без соответствующего исчерпания того, что питает ее. Если бы контактная теория была верна, то следовало бы отрицать равенство причины и действия. Но тогда был бы возможен и perpetuum mobile».

Но наибольшего обобщения достиг немецкий врач Юлиус Роберт Майер (1814–1878) – ученый с необыкновенными интуицией и воображением. Будучи судовым врачом, он провел физиологические наблюдения изменений цвета крови у матросов, перешедших из умеренного в тропический пояс. Майер пришел к выводу, что «температурная разница между собственным теплом организма и теплом окружающей среды должна находиться в количественном соотношении с разницей в цвете обоих видов крови – артериальной и венозной. Эта разница является выражением размера потребления кислорода или силы процесса сгорания, происходящего в организме» (подчеркнуто мною. – В.Д.).

Из области медицинских наблюдений Майер переходит к анализу физико-химических процессов и опирается при этом на закон сохранения сил. Свои размышления он оформил в виде статьи «О количественном и качественном определении сил» и послал в журнал. Редактор – известный физик К.Поггендорф – бросил статью неизвестного врача в корзину. Майер был вынужден печатать свои работы в журнале «Анналы химии и фармации», так что они стали известны физикам только после смерти автора.

Майер утверждал, что «движение, теплота, и, как мы намерены показать в дальнейшем, электричество представляют собой явления, которые могут быть сведены к единой силе, которые изменяются друг другом и переходят друг в друга по определенным законам». Он ставит принципиальной важности задачи на закон сохранения энергии, например: «Как высоко должен быть поднят определенный груз над поверхностью земли, чтобы его сила падения была эквивалентна нагреванию равного ему по весу количеству воды от 0 до 1 °?»

Майер вычисляет из опытов над «сжатием воздуха», что одна калория эквивалентна поднятию одного килограмма на 0,365 м. При этом он использует уравнение состояния идеальных газов и вычисляет разность теплоемкостей при постоянном давлении и постоянном объеме. Поэтому равенство с_p – с_v = R, где R – универсальная газовая постоянная, носит его имя.

vСвои выводы о сохранении сил природы при превращениях Майер переносит на органическую природу. В частности, он развивает мысль о значении процесса ассимиляции в растениях для поддержания жизнедеятельности организмов. Внушительны его аргументы в опровержение распространенной тогда в науке теории о существовании особой жизненной силы.

В сочинении «Динамика неба» законы сохранения переносятся на космические явления. Вот отрывок из этой книги: «Часто и удачно Солнце сравнивают с непрерывно звучащим колоколом. Но что же поддерживает звучание этого небесного тела, столь величественно и чудесно наполняющего небесные пространства своими лучами, что поддерживает его в вечно неослабевающей силе и юности? Что предохраняет его от полного истощения, от наступления равновесия, дабы ночь и смертельный холод не заполнили пространства нашей планетной системы? Всеобщий закон природы, не допускающий никаких исключений, гласит, что для образования тепла необходима известная затрата. Эту затрату, как бы разнообразна она ни была, всегда можно свести к двум главным категориям, а именно, она сводится либо к химическому материалу, либо к механической работе».

Статья подготовлена при поддержке кредитного потребительского кооператива «ДаНаЯ». Если Вы решили получить кредит для своих нужд, то оптимальным решением станет обратиться в кооператив «ДаНаЯ». Перейдя по ссылке: «помощь в получении кредита», вы сможете, не отходя от экрана монитора, узнать более подробную информацию о получении кредита и действующих акциях. В кооперативе «ДаНаЯ» работают только высококвалифицированные специалисты с огромным опытом работы с клиентами в сфере кредитования населения.

Рядом с Майером стоит имя Джоуля. С такой же целеустремленностью он шел к всестороннему экспериментальному обоснованию общности закона сохранения энергии. Выше говорилось о его классическом опыте по определению термического эквивалента работы. Но его первое исследование было посвящено превращению электричества в теплоту. В работе 1841 г. «О теплоте, выделяемой металлическими проводниками электричества и элементами батарей при электролизе» он приходит к известному закону: Q=I²Rt.

Далее Джоуль перешел к другому виду превращения энергии. В работе «Об электрическом происхождении теплоты горения» он показал, что количество теплоты, выделяемой током в цепи, тождественно теплоте, которая может быть получена непосредственным окислением составляющих цепь металлов, включая водород. Отсюда ученый заключил, что теплота, выделяющаяся во внешней цепи гальванического элемента, является результатом превращения теплоты химических реакций.

Экспериментами, где электрический ток одновременно выделяет теплоту и производит механическую работу, Джоуль доказывает, что энергия сохраняется и при сложных превращениях.

vВ серии работ 1843 г. «О тепловом эффекте магнитоэлектричества и механической величине тепла» Джоуль открывает, что теплота, выделяющаяся в нагрузке магнито-электрического генератора имеет своим источником механическую работу. Он заставляет вращаться катушку между полюсами сильного магнита с помощью падающих грузов. Катушка была помещена в стеклянную трубку с водой, последняя выполняла роль калориметра. Возбуждаемый в катушке индукционный ток приводил к выделению теплоты и повышению температуры воды. Зная массу грузов и высоту падения, можно было определить затраченную энергию, а по величине массы воды и повышению ее температуры – полученное количество теплоты, отсюда получалось соотношение между джоулем и калорией – термический эквивалент работы: 1Дж=0,24 кал.

Далее Джоуль изучает непосредственное превращение механической работы в теплоту. Продавливая воду через узкие трубки, он сравнивает произведенную работу и выделившееся количество теплоты. Затем он сжимает воздух и измеряет затраченную при этом работу и полученное повышение его температуры. И во всех случаях он обнаруживает пропорциональность выделившегося количества теплоты произведенной работе.

4. Первая точная формулировка закона. Переход к понятию энергии

Хотя факт сохранения сил природы их многообразных превращений был установлен целым рядом независимых экспериментов, он не имел точного выражения, поэтому оставался неким утверждением философского толка, а физики середины XIX в. скептически относились к таким утверждениям, тем более что публиковались они не профессионалами.

Необходимо было сформулировать закон в точных понятиях и дать ему математическое выражение. Это сделал Герман Гельмгольц (1821–1894).

Гельмгольц родился в Потсдаме, в семье учителя гимназии. Мать его происходила из семьи английских эмигрантов. Стесненный семейный бюджет не позволил талантливому юноше поступить в университет, пришлось выбрать карьеру врача. В казармах Постдама Гельмгольц начал физиологические исследования, одновременно изучая труды классиков физики.

Он быстро вышел на путь самостоятельного творчества и обобщений. Молодой военный врач публикует в 1847 г. книгу «О сохранении силы», которая сразу сделала его известным физиком. Однако это мало повлияло на его карьеру.

По рекомендации Гумбольта Гельмгольц получил место ассистента в анатомо-физиологическом музее Берлина, но его успехи в науке столь впечатляющи, что его через год приглашает Кеннингсбергский университет на должность профессора анатомии и физиологии.

Постепенно растет удельный вес физической тематики в его исследованиях, и Гельмгольц становится главой немецкой физической школы. Он поразительно разносторонен: наряду с работами по обоснованию закона сохранения энергии, исследования по термодинамике, по электродинамике химических процессов, по механике вихревых движений в жидкостях, оптические, физические и физиологические исследования, основополагающие труды по физиологии слуха и зрения. Он первый измерил теплообразование в мышцах, скорость распространения нервных импульсов. Вместе с тем Гельмгольц был блестящим популяризатором науки.

В поисках математической формулировки закона сохранения сил природы Гельмгольц опирался на последовательно механическую концепцию: материя представляет собой совокупность материальных точек, между которыми действуют центральные силы. Целью физической науки, согласно Гельмгольцу, является сведение явлений природы к движению и взаимодействию материальных точек, притягивающихся или отталкивающихся силами, зависящими от расстояния между ними.

Если исходить из такой модели материи, то все виды сил (энергии) можно свести к двум: живым силам движущихся материальных точек (энергии движения) и силам напряжения (энергии положения). Тогда закон сохранения сил (энергии) можно сформулировать так: «Когда тела природы действуют друг на друга с силами притяжения или отталкивания, не зависящими от времени и скорости, то сумма их живых сил и сил напряжения остается постоянной. Максимум работы, которую можно получить, является, таким образом, определенным, конечным».

М.Планк в своей книге «Принцип сохранения энергии» следующим образом поясняет идею Гельмгольца: «Преобразование принципа живой силы, принятое Гельмгольцем для того, чтобы превратить его в принцип сохранения силы, заключается в том, что в уравнение, выражающее соотношение живой силы L и работы А, произведенной действующими силами L + А = const, он вводит вместо понятия работы А понятие количества сил напряжения U, равное и противоположное по знаку величине работы А. Сила напряжения, так же как и работа, зависит только от мгновенного состояния системы, и вышеуказанное уравнение можно сформулировать следующим образом: сумма количества живой силы и силы напряжения остается неизменной во времени: L + А = const. Если мы эту сумму коротко обозначим как силу, заключенную в системе, то тем самым мы получим закон сохранения силы.

Как ни незначительным кажется, на первый взгляд, это преобразование, перспектива, которую он открывает во всех областях физики, чрезвычайно велика, ибо возможность его обобщения для любых явлений природы легко бросается в глаза. Главное основание для такого обобщения заключается в том, что принцип сохранения силы выступает параллельно с давно уже известным и, так сказать, перешедшим в инстинкт, принципом сохранения материи. Так же, как количество содержащейся в системе тел и измеряемой их весом материи не может быть никакими средствами уменьшено или увеличено, какие бы различные физические и химические превращения не происходили в системе, так и количество содержащейся в системе силы представляет собой самостоятельную, совершенно неизменную величину. Сила, так же как и материя, может быть представлена в многообразных формах, но прежде всего она проявляется в двух основных формах: как живая сила и как сила напряжения. Обе эти формы могут выступать различнейшим образом: живая сила – как видимое движение, как свет, теплота; сила напряжения – как поднятие тяжести, как упругое напряжение, как электрическое напряжение».

Особый интерес в этом пояснении представляет указание Планка на аналогию законов сохранения материи и энергии.

Сформулировав закон, Гельмгольц далее рассматривает его действенность во всех разделах физики. Один из примеров применения закона сохранения энергии, который он рассматривает в своем мемуаре «О сохранении силы», вошел в учебники физики: это вывод закона электромагнитной индукции, опирающийся на закон сохранения энергии.

Кроме Майера, Джоуля и Гельмгольца обоснованием закона сохранения силы и измерениями механического эквивалента теплоты занимался целый ряд других исследователей. Тем не менее вся эта гигантская волна интеллектуальных усилий не привлекала внимания маститых физиков. Резкий перелом произошел в начале второй половины XIX в., и он совпал со временем введения в лексикон физики понятия энергии.

Интерес к закону прогрессивно возрастал, естественно, стали задумываться над двойным использованием фундаментального понятия силы. Физики, конечно, не путали лейбницевскую «живую силу» с ньютоновской, но неудобство такого раздвоения понятия было очевидно. И тогда вспомнили, что еще в 1807 г. в «Лекциях по естественной философии» Т.Юнг вместо понятия «живой силы» пользовался понятием энергии. Последнее было единодушно принято ведущими физиками мира. В 1852 г. в работе «Динамическая теория тепла» В.Томсон дал первое определение энергии: «Под энергией материальной системы в определенном состоянии мы понимаем измеренную в механических единицах работы сумму всех действий, которые производятся вне системы, когда она переходит из этого состояния любым способом в произвольно выбранное нулевое состояние».

Несколько позже Максвелл дал простое и точное определение энергии как способности системы совершать работу, подчеркнув неразрывность связи понятий энергии и работы. Анализ этой связи привел в итоге к современному пониманию работы как процесса, приводящего к созданию источника энергии.

В 1883 г. Гельмгольц ввел в физику понятия свободной и связанной энергий. В своей классической работе «Термодинамика химических процессов» он писал: «Подобно тому, как теплота может превращаться в работу частично, так же в случае химических процессов должно быть принято разделение между частью сил химического сродства, способных к превращению в другие формы и той частью, которая может превращаться только в теплоту. Я позволю себе обозначить обе эти части энергии, как свободную и связанную энергии».

Г.Гесс (1802–1850) на основании многочисленных опытных исследований пришел к важному следствию закона сохранения энергии: тепловой эффект химических реакций не зависит от их промежуточных стадий, а определяется только начальным и конечным состояниями реагирующей системы.

Независимость процессов преобразования энергии от их промежуточных ступеней явилась одним из выражений общей характерной особенности закона сохранения, его своеобразного удобства: при научных исследованиях отпадала необходимость анализа стадий превращений энергии, их механизмов, качества материальных объектов, участвующих в этих превращениях.

Так постепенно начало складываться представление об энергии как общей количественной мере движения и взаимодействия всех видов материи. В изолированной системе энергия может переходить из одной формы в другую, но общее ее количество остается неизменным.

Закон сохранения энергии

Закон сохранения энергии гласит, что энергия не может быть ни создана, ни уничтожена — только преобразована из одной формы энергии в другую. Это означает, что система всегда имеет одинаковое количество энергии, если только она не добавляется извне. Это особенно сбивает с толку в случае неконсервативных сил, когда энергия преобразуется из механической энергии в тепловую, но общая энергия остается неизменной. Единственный способ использовать энергию — это преобразовывать энергию из одной формы в другую.

Таким образом, количество энергии в любой системе определяется по следующему уравнению:

[математика] U_ {T} = U_ {i} + W + Q [/ математика]

• [math] U_T [/ math] — это полная внутренняя энергия системы.
• [math] U_i [/ ​​math] — начальная внутренняя энергия системы.
• [математика] W [/ математика] — это работа, выполняемая системой или в ней.
• [math] Q [/ math] — тепло, добавляемое к системе или отводимое от нее.

Также можно определить изменение внутренней энергии системы, используя уравнение: [математика] \ Дельта U = W + Q [/ математика]

Это также утверждение первого закона термодинамики.

Хотя эти уравнения чрезвычайно эффективны, они могут затруднить понимание силы утверждения. Вывод состоит в том, что энергию нельзя создать из ничего. Общество должно откуда-то получать энергию, хотя есть много скрытых мест, откуда можно получить ее (некоторые источники являются первичным топливом, а некоторые источники — потоками первичной энергии).

В начале 20 ^-го -го века Эйнштейн понял, что даже масса является формой энергии (это называется эквивалентностью массы и энергии).8 м / с [/ математика].

Для дальнейшего чтения

Чтобы узнать больше о физике закона сохранения энергии, см. Раздел «Гиперфизика» или о том, как это связано с химией, см. Вики-страницу UC Davis по химии.

сбережения энергии | Определение и примеры

Посмотрите, как маятник, качающийся в шине, демонстрирует закон сохранения энергии

Объяснение принципа сохранения энергии.

Британская энциклопедия, Inc. Смотрите все видео по этой статье

Сохранение энергии , физический принцип, согласно которому энергия взаимодействующих тел или частиц в замкнутой системе остается постоянной. Первым видом энергии, который был распознан, была кинетическая энергия или энергия движения. При определенных столкновениях частиц, называемых упругими, сумма кинетической энергии частиц до столкновения равна сумме кинетической энергии частиц после столкновения. Понятие энергии постепенно расширялось и включало другие формы.Кинетическая энергия, теряемая телом, замедляющимся при движении вверх против силы тяжести, считалась преобразованной в потенциальную энергию или запасенную энергию, которая, в свою очередь, преобразуется обратно в кинетическую энергию по мере того, как тело ускоряется во время своего возвращения на Землю. . Например, когда маятник качается вверх, кинетическая энергия преобразуется в потенциальную. Когда маятник ненадолго останавливается в верхней точке своего колебания, кинетическая энергия равна нулю, а вся энергия системы находится в потенциальной энергии.Когда маятник опускается вниз, потенциальная энергия снова преобразуется в кинетическую. Всегда сумма потенциальной и кинетической энергии постоянна. Однако трение замедляет самые тщательно сконструированные механизмы, постепенно рассеивая их энергию. В 1840-х годах было окончательно показано, что понятие энергии можно расширить, включив в него тепло, генерируемое трением. Истинно сохраняемая величина — это сумма кинетической, потенциальной и тепловой энергии. Например, когда блок скользит по склону, потенциальная энергия преобразуется в кинетическую.Когда трение замедляет блок до остановки, кинетическая энергия преобразуется в тепловую. Энергия не создается и не разрушается, а просто меняет формы, переходя от потенциальной к кинетической и тепловой энергии. Эта версия принципа сохранения энергии, выраженная в самой общей форме, является первым законом термодинамики. Концепция энергии продолжала расширяться, включая энергию электрического тока, энергию, запасенную в электрическом или магнитном поле, и энергию в топливе и других химических веществах.Например, автомобиль движется, когда химическая энергия бензина преобразуется в кинетическую энергию движения.

Британская викторина

Викторина «Все о физике»

Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.

С появлением физики относительности (1905 г.) масса впервые была признана эквивалентом энергии. Полная энергия системы высокоскоростных частиц включает не только их массу покоя, но также очень значительное увеличение их массы вследствие их высокой скорости. После открытия теории относительности принцип сохранения энергии получил альтернативное название — сохранение массы-энергии или сохранение полной энергии.

Когда казалось, что принцип не работает, как это было в применении к типу радиоактивности, называемому бета-распад (спонтанный выброс электронов из атомных ядер), физики признали существование новой субатомной частицы, нейтрино, которая должна была унести недостающей энергии, а не отвергать принцип сохранения.Позже нейтрино было экспериментально обнаружено.

Однако энергосбережение — это больше, чем общее правило, которое остается в силе. Можно показать математически, что это следует из единообразия времени. Если бы один момент времени сильно отличался от любого другого момента, идентичные физические явления, происходящие в разные моменты времени, потребовали бы разного количества энергии, так что энергия не сохранялась бы.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.Подпишитесь сейчас

закон сохранения | Определение, примеры и факты

Закон сохранения , также называемый законом сохранения , в физике, принцип, который гласит, что определенное физическое свойство (т. Е. Измеряемая величина) не изменяется с течением времени в пределах изолированная физическая система. В классической физике законы этого типа управляют энергией, импульсом, угловым моментом, массой и электрическим зарядом. В физике элементарных частиц другие законы сохранения применяются к свойствам субатомных частиц, которые инвариантны во время взаимодействий.Важная функция законов сохранения состоит в том, что они позволяют предсказать макроскопическое поведение системы без необходимости рассматривать микроскопические детали протекания физического процесса или химической реакции.

Британская викторина

Викторина «Все о физике»

Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.

Посмотрите, как маятник в шине демонстрирует закон сохранения энергии.

Объяснение принципа сохранения энергии.

Encyclopædia Britannica, Inc. Посмотреть все видео к этой статье

Сохранение энергии подразумевает, что энергия не может быть ни создана, ни разрушена, хотя она может быть изменена из одной формы (механической, кинетической, химической и т. Д.) В другую. Таким образом, в изолированной системе сумма всех форм энергии остается постоянной.Например, падающее тело имеет постоянное количество энергии, но форма энергии меняется с потенциальной на кинетическую. Согласно теории относительности энергия и масса эквивалентны. Таким образом, массу покоя тела можно рассматривать как форму потенциальной энергии, часть которой может быть преобразована в другие формы энергии.

Сохранение массы подразумевает, что материя не может быть ни создана, ни разрушена — то есть процессы, которые изменяют физические или химические свойства веществ в изолированной системе (такие как преобразование жидкости в газ), оставляют общую массу неизменной.Строго говоря, масса не является сохраняющейся величиной. Однако, за исключением ядерных реакций, преобразование массы покоя в другие формы массы-энергии настолько мало, что с высокой степенью точности можно считать, что масса покоя сохраняется. Оба закона сохранения массы и сохранения энергии могут быть объединены в один закон сохранения массы-энергии.

Сохранение количества движения выражает тот факт, что движущееся тело или система тел сохраняет свой полный импульс, произведение массы и векторной скорости, если к нему не приложена внешняя сила.В изолированной системе (такой как Вселенная) нет внешних сил, поэтому импульс всегда сохраняется. Поскольку импульс сохраняется, его компоненты в любом направлении также будут сохранены. Применение закона сохранения импульса важно при решении задач столкновения. Работа ракет демонстрирует сохранение количества движения: увеличенный поступательный импульс ракеты равен импульсу выбрасываемых выхлопных газов, но противоположен по знаку.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.Подпишитесь сейчас

Сохранение момента количества движения вращающихся тел аналогично сохранению количества движения. Угловой момент — это векторная величина, сохранение которой выражает закон, согласно которому вращающееся тело или система продолжает вращаться с той же скоростью, если к нему не приложена скручивающая сила, называемая крутящим моментом. Угловой момент каждой частицы материи состоит из произведения ее массы, расстояния от оси вращения и составляющей скорости, перпендикулярной линии, идущей от оси.

Сохранение заряда означает, что общее количество электрического заряда в системе не меняется со временем. На субатомном уровне заряженные частицы могут быть созданы, но всегда парами с равным положительным и отрицательным зарядом, так что общее количество заряда всегда остается постоянным.

В физике элементарных частиц другие законы сохранения применяются к определенным свойствам ядерных частиц, таким как барионное число, лептонное число и странность. Такие законы применяются в дополнение к законам массы, энергии и импульса, встречающимся в повседневной жизни, и их можно рассматривать как аналог сохранения электрического заряда. См. Также симметрию .

Законы сохранения энергии, импульса и момента количества движения происходят из классической механики. Тем не менее, все остается верным в квантовой механике и релятивистской механике, которые заменили классическую механику как наиболее фундаментальный из всех законов. В самом глубоком смысле три закона сохранения выражают, соответственно, факты, согласно которым физика не меняется с течением времени, смещением в пространстве или вращением в пространстве.

Закон сохранения энергии Примеры

Закон сохранения энергии — это закон физики, который гласит, что энергия не может быть создана или уничтожена, а только преобразована из одной формы в другую или передана от одного объекта к другому.Этот закон преподается учащимся средних и старших классов на уроках физики, физики и химии.

Понимание закона сохранения энергии

Определение закона сохранения энергии подчеркивает, что энергия не является чем-то, что можно разрушить или создать. Важно понимать, что это на самом деле означает. Было бы неправильно сказать, что целью эксперимента было бы получение энергии, поскольку это потребовало бы усилий по созданию чего-то, что невозможно создать.Вместо этого энергия постоянно преобразуется, чтобы ее можно было использовать. Например, солнечные панели не создают солнечную энергию. Они используют энергию солнца и преобразуют ее в другой вид энергии (электричество).

Примеры на каждый день: закон сохранения энергии

Многие примеры, иллюстрирующие закон сохранения энергии, можно увидеть в повседневной жизни. Просмотрите эти знакомые примеры передачи энергии, чтобы составить четкое представление о том, как научный закон сохранения энергии влияет на повседневные явления.

Сохранение энергии Примеры с участием людей

Энергия может передаваться между людьми или от людей к объектам. Все эти примеры иллюстрируют закон сохранения энергии.

• Келли побежала через комнату и столкнулась со своим братом, повалив его на пол. Кинетическая энергия, которой она обладала из-за своего движения, была передана ее брату, заставив его двигаться.
• Два футболиста столкнулись на поле, и оба полетели назад.Энергия передавалась от каждого игрока к другому, отправляя их в том направлении, в котором они бежали.
• Когда вы толкаете книгу по столу, энергия движущейся руки передается от вашего тела к книге, заставляя книгу двигаться.
  
• При ударе ногой по мячу, стоящему на земле, энергия передается от тела бьющего к мячу, приводя его в движение.
• Сэм переставлял мебель, и ему потребовалась помощь, чтобы сдвинуть тяжелый диван.Его брат подошел, и вместе они смогли толкнуть диван через всю комнату. Когда диван скользил по деревянному полу, энергия передавалась от мужчин к предмету мебели.
• Пальцы, ударяющие по клавишам пианино, передают энергию от руки игрока к клавишам.
• Билли ударил боксерскую грушу, передавая энергию от руки к стационарной сумке.
• Бет так сильно ударилась о стену, что проделала в ней дыру. Энергия передавалась от тела Бет к гипсокартону, заставляя его двигаться.

Примеры экономии энергии от объекта к объекту

Когда два объекта сталкиваются друг с другом, энергия передается между двумя объектами.

• При игре в пул биток выполняется по неподвижному шару-восьмерке. Биток обладает энергией. Когда биток попадает в шар-восьмерку, энергия передается от шара-восьмерки, заставляя его двигаться. Биток теряет энергию из-за того, что энергия, которая была передана шару-восьмерке, замедляется.
• При игре в мяч для игры на лужайке в бочче бросается маленький мяч с намерением попасть в более крупные шары и заставить их двигаться. Когда больший шар движется из-за того, что в него попал маленький шар, энергия передается от маленького шара к большему.
• Бейсбольный мяч попадает в окно в доме, разбивая стекло. Энергия шара передавалась стеклу, заставляя его разлетаться на части и лететь в разных направлениях.
• Когда движущийся автомобиль ударяется о припаркованный автомобиль и заставляет припаркованный автомобиль двигаться, механическая энергия передается от движущегося автомобиля к припаркованному.
• Клэр бросила шар, который ударил в вазу ее матери, опрокинув ее. Энергия передавалась от движущегося шара к неподвижной вазе, заставляя вазу двигаться.
• При наезде на дорожный знак знак упадет. Энергия будет передаваться от движущегося автомобиля к неподвижному знаку, заставляя знак двигаться.
• Когда шар для боулинга сталкивается с неподвижными кеглями, энергия передается от шара к кеглям. Энергия не теряется.
• Автомобиль при ударе о бордюр разлетелся на части.Энергия от движущегося автомобиля передавалась неподвижному цементу, заставляя его двигаться.

Другие примеры сохранения энергии

Многие другие ситуации иллюстрируют, как энергия может переходить из одной формы в другую или передаваться между объектами.

• Вода может производить электричество. Когда вода падает с неба, она преобразует потенциальную энергию в кинетическую. Эта энергия затем используется для вращения турбины генератора для производства электроэнергии. Потенциальная энергия воды в плотине может быть преобразована в кинетическую энергию.
• Потенциальная энергия из нефти или газа — это вид химической энергии. Его энергию можно использовать для обогрева домов, офисов и других зданий, чтобы согреться зимой.
• Лампочки преобразуют электрическую энергию в свет, который освещает темные места.
• Кошка, сидящая на самой высокой ветке дерева, обладает так называемой потенциальной энергией. Если кошка упадет с ветки и упадет на землю, ее потенциальная энергия теперь преобразуется в кинетическую.
  
• Собака налетела на елку и свалила ее. Во время удара энергия передавалась от движущейся собаки к неподвижному дереву, заставляя дерево двигаться.

Узнать больше об энергии

Вышеприведенные примеры закона сохранения энергии показывают, насколько банальна эта физическая концепция в повседневной жизни. Теперь, когда вы знакомы с этим научным законом, найдите время, чтобы узнать о различных типах энергии.

Сохранение энергии | Физика

Цели обучения

К концу этого раздела вы сможете:

• Объясните закон сохранения энергии.
• Опишите некоторые из множества форм энергии.
• Определите эффективность процесса преобразования энергии как долю оставшейся полезной энергии или работы, а не преобразованную, например, в тепловую энергию.

Закон сохранения энергии

Энергия, как мы уже отметили, сохраняется, что делает ее одной из важнейших физических величин в природе. Закон сохранения энергии можно сформулировать следующим образом:

Полная энергия постоянна в любом процессе.Он может меняться по форме или передаваться из одной системы в другую, но общая сумма остается неизменной.

Мы исследовали некоторые формы энергии и способы ее передачи из одной системы в другую. Это исследование привело к определению двух основных типов энергии — механической энергии (KE + PE) и энергии, передаваемой через работу, выполняемую неконсервативными силами ( W _nc ). Но энергия принимает множество других форм, проявляясь многими различными способами, и нам нужно иметь возможность иметь дело со всеми этими формами, прежде чем мы сможем написать уравнение для приведенного выше общего утверждения сохранения энергии.

Другие формы энергии, помимо механической энергии

На этом этапе мы имеем дело со всеми другими формами энергии, объединяя их в одну группу под названием другая энергия (OE). Тогда мы можем сформулировать сохранение энергии в виде уравнения как KE _i + PE _i + W _nc + OE _i = KE _f + PE _f + OE _f .

Все виды энергии и работы могут быть включены в это очень общее заявление о сохранении энергии.Кинетическая энергия — KE, работа, совершаемая консервативной силой, представлена ​​PE, работа, совершаемая неконсервативными силами, — W _nc , а все другие энергии включены как OE. Это уравнение применимо ко всем предыдущим примерам; в этих ситуациях OE было постоянным, поэтому оно вычиталось и не учитывалось напрямую.

Установление соединений: полезность принципа энергосбережения

Тот факт, что энергия сохраняется и имеет множество форм, делает ее очень важной.Вы обнаружите, что энергия обсуждается во многих контекстах, потому что она участвует во всех процессах. Также станет очевидным, что многие ситуации лучше всего понять с точки зрения энергии и что проблемы часто легче всего концептуализировать и решать, рассматривая энергию.

Когда OE играет роль? Один пример происходит, когда человек ест. Пища окисляется с выделением углекислого газа, воды и энергии. Часть этой химической энергии преобразуется в кинетическую энергию, когда человек движется, в потенциальную энергию, когда человек меняет высоту, и в тепловую энергию (другая форма OE).

Некоторые из многих форм энергии

Какие еще формы энергии? Вы, наверное, можете назвать ряд форм энергии, которые еще не обсуждались. Многие из них будут рассмотрены в следующих главах, но давайте подробно остановимся на некоторых здесь. Электрическая энергия — это обычная форма, которая преобразуется во многие другие формы и действительно работает в широком диапазоне практических ситуаций. Топливо, такое как бензин и продукты питания, несут химическую энергию , которая может быть передана системе путем окисления.Химическое топливо также может производить электрическую энергию, например, в батареях. Батареи, в свою очередь, могут производить свет, который представляет собой очень чистую форму энергии. Фактически, большинство источников энергии на Земле — это запасенная энергия из энергии, которую мы получаем от Солнца. Мы иногда называем это излучением или электромагнитным излучением, которое включает в себя видимый свет, инфракрасное и ультрафиолетовое излучение. Ядерная энергия происходит из процессов, которые преобразуют измеримые количества массы в энергию.Ядерная энергия преобразуется в энергию солнечного света, в электрическую энергию на электростанциях и в энергию передачи тепла и взрыва в оружии. Атомы и молекулы внутри всех объектов находятся в беспорядочном движении. Эта внутренняя механическая энергия от случайных движений называется тепловой энергией , потому что она связана с температурой объекта. Эти и все другие формы энергии могут быть преобразованы друг в друга и могут работать.

В таблице 1 указано количество энергии, накопленной, используемой или высвобождаемой различными объектами и в различных явлениях.Диапазон энергий, разнообразие типов и ситуаций впечатляет.

Стратегии решения проблем для энергетики

Вы найдете следующие стратегии решения проблем полезными всякий раз, когда имеете дело с энергией. Стратегии помогают в организации и укреплении энергетических концепций. Фактически, они используются в примерах, представленных в этой главе. Знакомые общие стратегии решения проблем, представленные ранее, включающие определение физических принципов, известных и неизвестных, проверочные единицы и т. Д., По-прежнему актуальны.

Шаг 1. Определите интересующую систему и определите, какая информация предоставляется и какое количество должно быть рассчитано. Эскиз поможет.

Шаг 2. Изучите все задействованные силы и определите, знаете ли вы или получаете ли вы потенциальную энергию от работы, выполняемой этими силами. Затем используйте шаг 3 или шаг 4.

Шаг 3. Если вы знаете потенциальные энергии сил, которые входят в проблему, тогда все силы консервативны, и вы можете применить закон сохранения механической энергии просто в терминах потенциальной и кинетической энергии.Уравнение, выражающее сохранение энергии: KE _i + PE _i = KE _f + PE _f .

Шаг 4. Если вы знаете потенциальную энергию только для некоторых сил, возможно потому, что некоторые из них неконсервативны и не имеют потенциальной энергии, или если есть другие энергии, которые нелегко трактовать с точки зрения силы и работы, то необходимо использовать закон сохранения энергии в самом общем виде.

KE _i + PE _i + W _NC + OE _i = KE _f + PE _f + OE _f .

В большинстве задач один или несколько членов равны нулю, что упрощает их решение. Не рассчитывайте W _c , работа сделана консервативными силами; он уже включен в условия PE.

Шаг 5. Вы уже определили типы работы и энергии (на шаге 2). Перед тем как найти неизвестное, по возможности исключите члены , чтобы упростить алгебру. Например, выберите h = 0 в начальной или конечной точке, чтобы PE _g был равен нулю.Затем привычным способом решите неизвестное.

Шаг 6. Проверьте ответ, чтобы убедиться, что он разумный . Решив проблему, еще раз проверьте формы работы и энергии, чтобы убедиться, что вы правильно составили уравнение сохранения энергии. Например, работа, выполняемая против трения, должна быть отрицательной, потенциальная энергия внизу холма должна быть меньше, чем наверху, и так далее. Также убедитесь, что полученное числовое значение является разумным.Например, конечная скорость скейтбордиста, спускающегося по рампе высотой 3 м, разумно может составлять 20 км / ч, но , а не 80 км / ч.

Преобразование энергии

Рис. 1. Солнечная энергия преобразуется в электрическую с помощью солнечных элементов, которые используются для запуска двигателя в этом летательном аппарате, работающем на солнечной энергии. (кредит: НАСА)

Преобразование энергии из одной формы в другую происходит постоянно. Химическая энергия пищи преобразуется в тепловую в процессе метаболизма; световая энергия преобразуется в химическую энергию посредством фотосинтеза.В более крупном примере химическая энергия, содержащаяся в угле, преобразуется в тепловую энергию, когда он сгорает, превращая воду в пар в бойлере. Эта тепловая энергия пара, в свою очередь, преобразуется в механическую энергию при вращении турбины, которая соединена с генератором для производства электроэнергии. (Во всех этих примерах не вся начальная энергия преобразуется в упомянутые формы. Этот важный момент обсуждается позже в этом разделе.)

Другой пример преобразования энергии происходит в солнечном элементе.Солнечный свет, падающий на солнечный элемент (см. Рисунок 1), производит электричество, которое, в свою очередь, может использоваться для запуска электродвигателя. Энергия преобразуется из первичного источника солнечной энергии в электрическую, а затем в механическую.

Таблица 1. Энергия различных предметов и явлений
Объект / явление	Энергия в джоулях
Большой взрыв	10 68
Энергия, выделяемая при сверхновой	10 44
Синтез всего водорода в океанах Земли	10 34
Годовое мировое потребление энергии	4 × 10 20
Большая термоядерная бомба (9 мегатонн)	3.8 × 10 16
1 кг водорода (синтез с гелием)	6,4 × 10 14
1 кг урана (ядерное деление)	8,0 × 10 13
Делящаяся бомба размером с Хиросиму (10 килотонн)	4,2 × 10 13
Авианосец водоизмещением тонн, скорость 30 узлов	1,1 × 10 10
1 баррель сырой нефти	5.9 × 10 9
1 тонна в тротиловом эквиваленте	4,2 × 10 9
1 галлон бензина	1,2 × 10 8
Ежедневное потребление электроэнергии в домашних условиях (развитые страны)	7 × 10 7
Суточное потребление пищи взрослыми (рекомендуется)	1,2 × 10 7
Автомобиль массой 1000 кг, скорость 90 км / ч	3,1 × 10 5
1 г жира (9.3 ккал)	3,9 × 10 4
Реакция гидролиза АТФ	3,2 × 10 4
1 г углеводов (4,1 ккал)	1,7 × 10 4
1 г белка (4,1 ккал)	1,7 × 10 4
Теннисный мяч со скоростью 100 км / ч	22
Комар (10 −2 г при 0,5 м / с)	1,3 × 10 −6
Одиночный электрон в пучке телевизионной трубки	4.0 × 10 −15
Энергия разрыва одной цепи ДНК	10 −19

КПД

Даже если энергия сохраняется в процессе преобразования энергии, выход полезной энергии или работы будет меньше, чем потребляемая энергия. Эффективность Eff процесса преобразования энергии определяется как

[латекс] \ displaystyle \ text {Эффективность} (Eff) = \ frac {\ text {полезная энергия или выход работы}} {\ text {общее количество потребляемой энергии}} = \ frac {W _ {\ text {out}}} {E _ {\ text {in}}} \\ [/ latex]

В таблице 2 перечислены некоторые показатели эффективности механических устройств и деятельности человека.Например, на угольной электростанции около 40% химической энергии угля становится полезной электрической энергией. Остальные 60% преобразуются в другие (возможно, менее полезные) формы энергии, такие как тепловая энергия, которая затем выделяется в окружающую среду через дымовые газы и градирни.

Таблица 2. Эффективность человеческого тела и механических устройств
Деятельность / устройство	КПД (%)
Велоспорт и скалолазание	20
Плавание на поверхности	2
Плавание под водой	4
Лопатой	3
Тяжелая атлетика	9
Паровой двигатель	17
Бензиновый двигатель	30
Дизельный двигатель	35
Атомная электростанция	35
Угольная электростанция	42
Электродвигатель	98
Компактный люминесцентный свет	20
Обогреватель газовый (жилой)	90
Солнечный элемент	10

Исследования PhET: массы и пружины

Реалистичная лаборатория масс и пружин.Подвесьте массы к пружинам и отрегулируйте жесткость и демпфирование пружины. Вы даже можете замедлить время. Перенесите лабораторию на разные планеты. На диаграмме показаны кинетическая, потенциальная и тепловая энергии каждой пружины.

Щелкните, чтобы запустить моделирование.

Сводка раздела

• Закон сохранения энергии гласит, что полная энергия постоянна в любом процессе. Энергия может меняться по форме или передаваться из одной системы в другую, но общее количество остается неизменным.
• Когда рассматриваются все формы энергии, сохранение энергии записывается в форме уравнения как KE _i + PE _i + W _nc + OE _i = KE _f + PE _f + OE _f , где OE — , все другие виды энергии , кроме механической энергии.
• Обычно встречающиеся формы энергии включают электрическую энергию, химическую энергию, лучистую энергию, ядерную энергию и тепловую энергию.
• Энергия часто используется для выполнения работы, но невозможно преобразовать всю энергию системы для работы.
• Эффективность Eff машины или человека определяется как [латекс] \ text {Eff} = \ frac {{W} _ {\ text {out}}} {{E} _ {\ text {in} }} \\ [/ latex], где Вт, , _из — полезная рабочая мощность, а E, , _в — потребляемая энергия.

Концептуальные вопросы

1. Рассмотрим следующий сценарий. Автомобиль, для которого трение не является незначительным, ускоряется в состоянии покоя вниз по склону, заканчиваясь бензином после небольшого расстояния. Водитель позволяет машине двигаться дальше вниз по склону, затем вверх и по небольшому гребню.Затем он спускается с холма на заправочную станцию, тормозит до остановки и заправляет бак бензином. Определите формы энергии, которые есть в машине, и то, как они изменяются и передаются в этой серии событий. (См. Рисунок 2.)

   Рис. 2. Автомобиль, испытывающий существенное трение, едет вниз по склону, преодолевает небольшой гребень, затем снова спускается с горы и останавливается на заправочной станции.

2. Автомобиль, испытывающий существенное трение, спускается с холма, преодолевает небольшой гребень, затем снова спускается с холма и останавливается на заправке.
3. Автомобиль едет по инерции, двигается по гребню, затем снова спускается с горы и, наконец, останавливается на заправке. Каждая из этих позиций помечена стрелкой, направленной вниз.
4. Опишите передачу энергии и трансформацию копья, начиная с момента, когда спортсмен поднимает копье, и заканчивая тем, что копье застревает в земле после броска.
5. Нарушают ли устройства с КПД меньше единицы закон сохранения энергии? Объяснять.
6. Перечислите четыре различных формы или типа энергии. Приведите один пример преобразования каждой из этих форм в другую.
7. Перечислите преобразования энергии, которые происходят при езде на велосипеде.

Задачи и упражнения

1. Используя значения из Таблицы 1, сколько молекул ДНК могло бы быть разрушено энергией, переносимой одним электроном в луче старомодной телевизионной трубки? (Эти электроны сами по себе не опасны, но они создают опасные рентгеновские лучи.Более поздние модели ламповых телевизоров имели экранирование, которое поглощало рентгеновские лучи до того, как они ускользнули и подверглись воздействию зрителей.)
2. Используя соображения энергии и допуская незначительное сопротивление воздуха, покажите, что камень, брошенный с моста на высоте 20,0 м над водой с начальной скоростью 15,0 м / с, ударяется о воду со скоростью 24,8 м / с независимо от направления метания.
3. Если бы энергия термоядерных бомб использовалась для обеспечения мировых энергетических потребностей, сколько из 9-мегатоннных бомб потребовалось бы для годового запаса энергии (с использованием данных из Таблицы 1)? Это не так надумано, как может показаться — существуют тысячи ядерных бомб, и их энергия может быть захвачена в результате подземных взрывов и преобразована в электричество, как это делает природная геотермальная энергия.
4. (a) Использование синтеза водорода для получения энергии — мечта, которая может быть реализована в следующем столетии. Термоядерный синтез будет относительно чистым и почти безграничным источником энергии, как видно из таблицы 1. Чтобы проиллюстрировать это, подсчитайте, сколько лет нынешние энергетические потребности мира могут быть обеспечены одной миллионной частью энергии синтеза водорода в Мировом океане. (б) Как это время соотносится с исторически значимыми событиями, такими как продолжительность стабильной экономической системы?

Глоссарий

закон сохранения энергии: общий закон, согласно которому полная энергия постоянна в любом процессе; энергия может меняться по форме или передаваться из одной системы в другую, но общее количество остается прежним

электрическая энергия: энергия, переносимая потоком заряда

химическая энергия: энергия вещества, хранящаяся в связях между атомами и молекулами, которая может высвобождаться в химической реакции

лучистая энергия: энергия, переносимая электромагнитными волнами

ядерная энергия: энергия, выделяемая в результате изменений в атомных ядрах, таких как слияние двух легких ядер или деление тяжелого ядра

тепловая энергия: энергия внутри объекта из-за случайного движения его атомов и молекул, которая составляет температуру объекта

эффективность: мера эффективности затраченной энергии для выполнения работы; полезная энергия или работа, деленная на общее количество потребляемой энергии

Избранные решения проблем и упражнения

1.2} = 24,8 \ text {м / с} \\ [/ latex]

4. (а) 25 × 10 ⁶ лет; (б) Это намного больше, чем человеческие масштабы времени.

---

Сохранение энергии

Сохранение энергии — фундаментальное понятие физики. вместе с сохранение массы и сохранение импульса. В некоторой проблемной области количество энергии остается постоянным. и энергия не создается и не разрушается. Энергия может быть преобразована из одна форма в другую (потенциальная энергия может быть преобразована в кинетическую энергия), но полная энергия внутри домена остается фиксированной.

Термодинамика — это раздел физики который имеет дело с энергией и работой системы. Как упоминалось в слайд свойств газа, термодинамика только с крупномасштабным откликом системы, который мы можем наблюдать и измерять в экспериментах. В ракетостроении мы больше всех интересуется термодинамикой при изучении двигательные установки и понимание высокоскоростных потоков.

На некоторых отдельных слайдах мы обсудили состояние статического газа, свойства которые определяют состояние, и первый закон термодинамики применительно к любой системе в целом.На этом слайде мы выводим полезную форму уравнения сохранения энергии для газа, начиная с первого закона термодинамики. Если называть внутреннюю энергию газа E , то работа, выполненная газом W , и тепло, переданное газу Q , тогда первый закон термодинамики указывает, что между состоянием «1» и состояние «2»:

E2 — E1 = Q — W

Аэрокосмические инженеры обычно упрощают термодинамический анализ с использованием интенсивных переменных; переменные, не зависящие от масса газа.Мы называем эти переменные конкретный переменные. Мы создаем «конкретную» переменную, беря свойство, чье значение зависит от массы системы и деления ее на массу системы. Многие из государственных объектов, перечисленных на этом слайде, например работа и внутренняя энергия зависят от общей массы газа. Мы будем использовать «специфические» версии этих переменных. Инженеры обычно используют строчные буквы для обозначения «конкретных». версия переменной. Тогда наше первое уравнение закона становится:

e2 — e1 = q — w

Поскольку мы рассматриваем движущийся газ, мы добавляем термин удельной кинетической энергии к внутренней энергии на левой стороне.2) / 2

и уравнение первого закона становится:

e2 — e1 + k2 — k1 = q — w

Есть две части конкретной работы для движущийся газ. Некоторые работы, называемые валковыми работами (wsh) , являются используется для перемещения жидкости или вращения вала, в то время как остальная часть работа идет на изменение состояния газ. Для давление p и удельный объем v , работа дана по:

w = (p * v) 2 — (p * v) 1 + wsh

Подставляя:

e2 — e1 + k2 — k1 = q — (p * v) 2 + (p * v) 1 — wsh

Если мы проведем небольшую алгебру по первому закону термодинамики, мы можем начать группировать некоторые члены уравнений.2/2

Полная удельная энтальпия аналогична полному давлению в Уравнение Бернулли; оба выражения включают «статическое» значение плюс половину квадрата скорость.

Последняя, ​​наиболее полезная форма уравнения энергии: дано в красной рамке.

ht2 — ht1 = q — wsh

Для компрессора или силовая турбина, внешнего тепла нет поток в газ и член «q» установлен равным нулю. в горелки, работы не производятся, а «wsh» срок установлен на ноль.

---

Деятельность:

---

Экскурсии

---

Навигация ..

Руководство для начинающих Домашняя страница

Сохранение энергии — Энциклопедия Нового Света

Эта статья посвящена закону сохранения энергии в физике.

В физике закон сохранения энергии утверждает, что общее количество энергии в изолированной системе остается постоянным.На основании этого закона ученые пришли к выводу, что в изолированной системе энергия не создается и не уничтожается, но она может менять форму. Например, потенциальная энергия может быть преобразована в кинетическую энергию, а кинетическая энергия может стать тепловой энергией.

Понимая этот закон, инженеры могут проектировать машины, которые могут использовать энергию для производства работы. Например, тепловая энергия (или тепло, выделяемое при сжигании топлива) может использоваться для привода турбины, которая, в свою очередь, может использоваться для выработки электроэнергии.Кроме того, на основании этого закона можно сделать вывод, что вечные двигатели могут работать только в том случае, если они не доставляют энергию в свое окружение, а устройства, которые производят больше энергии, чем вложено в них, невозможны. Однако с формулировкой теории относительности, сформулированной Альбертом Эйнштейном, ученые теперь рассматривают сохранение энергии как часть более крупного закона, а именно сохранения «массы-энергии».

История

Древние философы предполагали сохранение некой основной субстанции, из которой все сделано.Например, Фалес Милетский думал, что это вода.

В 1638 году Галилей опубликовал свой анализ нескольких ситуаций, включая знаменитый «прерванный маятник», который можно описать (на современном языке) как консервативное преобразование потенциальной энергии в кинетическую и обратно. Однако Галилей не описал этот процесс в современных терминах и, опять же, не может быть признан за решающее понимание. Готфрид Вильгельм Лейбниц в 1676–1689 годах первым попытался математически сформулировать вид энергии, который связан с движением (кинетическая энергия).{2}}

сохранялось до тех пор, пока массы не взаимодействовали. Он назвал это количество vis viva или жизненной силой системы. Принцип представляет собой точное заявление о приблизительном сохранении кинетической энергии в ситуациях, когда нет трения. Многие физики в то время считали, что сохранение импульса, которое выполняется даже в системах с трением, определяется импульсом:

∑imivi {\ displaystyle \, \! \ Sum _ {i} m_ {i} v_ { i}}

было сохраненным vis viva .Позже было показано, что при определенных условиях обе величины сохраняются одновременно, например, при упругих столкновениях.

В основном инженеры, такие как Джон Смитон, Питер Эварт, Карл Хотцманн, Густав-Адольф Хирн и Марк Сегин, возражали против того, что сохранение импульса само по себе недостаточно для практических расчетов, и использовали принцип Лейбница. Этот принцип также отстаивали некоторые химики, такие как Уильям Хайд Волластон. Такие ученые, как Джон Плейфейр, поспешили указать на то, что кинетическая энергия явно не сохраняется.Это очевидно для современного анализа, основанного на втором законе термодинамики, но в восемнадцатом и девятнадцатом веках судьба потерянной энергии все еще была неизвестна. Постепенно возникло подозрение, что тепло, неизбежно генерируемое движением при трении, было другой формой vis viva . В 1783 году Антуан Лавуазье и Пьер-Симон Лаплас рассмотрели две конкурирующие теории vis viva и теорию калорийности. ^[1] Наблюдения графа Рамфорда за выделением тепла во время сверления орудий в 1798 году добавили веса мнению о том, что механическое движение может быть преобразовано в тепло, и (что не менее важно), что преобразование было количественным и могло быть предсказано (с учетом универсальная константа преобразования кинетической энергии в тепло).{2}}

, который можно понимать как нахождение точного значения константы преобразования кинетической энергии в работу, в значительной степени был результатом работы Гаспара-Гюстава Кориолиса и Жана-Виктора Понселе в период 1819–1839 гг. Первый назвал количество Quantité de travail (количество работы), а второй — travail mécanique (механическая работа), и оба отстаивали его использование в инженерных расчетах.

В статье Über die Natur der Wärme, , опубликованной в Zeitschrift für Physik в 1837 году, Карл Фридрих Мор дал одно из первых общих утверждений доктрины сохранения энергии словами: «Помимо 54 известных химических элемента есть в физическом мире только один агент, и он называется Kraft [энергия или работа].В зависимости от обстоятельств он может проявляться как движение, химическое сродство, сцепление, электричество, свет и магнетизм; и из любой из этих форм он может быть преобразован в любую из других ».

Ключевым этапом в развитии современного принципа сохранения была демонстрация механического эквивалента тепла . Теория калорийности утверждала, что тепло может ни создаваться, ни разрушаться, но сохранение энергии влечет за собой противоположный принцип, согласно которому тепло и механическая работа взаимозаменяемы.

Принцип механической эквивалентности впервые был сформулирован в его современной форме немецким хирургом Юлиусом Робертом фон Майером. ^[2] Майер пришел к своему заключению во время путешествия в Голландскую Ост-Индию, где он обнаружил, что кровь его пациентов была более темно-красной, потому что они потребляли меньше кислорода и, следовательно, меньше энергии, чтобы поддерживать температуру своего тела в более жаркую погоду. климат. Он обнаружил, что тепло и механическая работа являются формами энергии, а позже, улучшив свои познания в физике, он вычислил количественное соотношение между ними.

Аппарат Джоуля для измерения механического эквивалента тепла. Нисходящий груз, прикрепленный к струне, заставляет лопасть, погруженную в воду, вращаться.

Между тем, в 1843 году Джеймс Прескотт Джоуль независимо открыл механический эквивалент в серии экспериментов. В самом известном, ныне называемом «аппаратом Джоуля», нисходящий груз, прикрепленный к струне, заставлял лопасть, погруженную в воду, вращаться. Он показал, что гравитационная потенциальная энергия, теряемая весом при спуске, равна тепловой энергии (теплу), полученной водой за счет трения о лопасть.

В период 1840–1843 годов подобная работа проводилась инженером Людвигом А. Колдингом, хотя она была мало известна за пределами его родной Дании.

Работы Джоуля и Майера страдали от сопротивления и пренебрежения, но именно работа Джоуля, возможно, несправедливо, в конечном итоге получила более широкое признание.

В 1844 году Уильям Роберт Гроув постулировал связь между механикой, теплом, светом, электричеством и магнетизмом, рассматривая их все как проявления одной «силы» ( энергия, в современных терминах).Гроув опубликовал свои теории в своей книге The Correlation of Physical Force . ^[3] В 1847 г., опираясь на более ранние работы Джоуля, Сади Карно и Эмиля Клапейрона, Герман фон Гельмгольц пришел к выводам, аналогичным выводам Гроув, и опубликовал свои теории в своей книге Über die Erhaltung der Kraft ( On the Conservation of Force, 1847). Общее современное признание этого принципа проистекает из этой публикации.

В 1877 году Питер Гатри Тейт утверждал, что принцип был основан сэром Исааком Ньютоном на основе творческого прочтения предложений 40 и 41 из Philosophiae Naturalis Principia Mathematica .Сейчас это считается не более чем примером истории вигов.

Первый закон термодинамики

Энтропия — это функция количества тепла, которое показывает возможность преобразования этого тепла в работу.

Для термодинамической системы с фиксированным числом частиц первый закон термодинамики можно сформулировать как:

δQ = dU + δW {\ displaystyle \ delta Q = \ mathrm {d} U + \ delta W \, }, или, что эквивалентно, dU = δQ − δW {\ displaystyle \ mathrm {d} U = \ delta Q- \ delta W \,},

, где δQ {\ displaystyle \ delta Q} — количество энергии, добавленной к системы в процессе нагрева, δW {\ displaystyle \ delta W} — это количество энергии, потерянное системой из-за работы, выполняемой системой в ее окружении, а dU {\ displaystyle \ mathrm {d} U} — увеличение внутренняя энергия системы.

δ перед термином «тепло» и «работа» используются для обозначения того, что они описывают приращение энергии, которое следует интерпретировать несколько иначе, чем приращение внутренней энергии dU {\ displaystyle \ mathrm {d} U}. Работа и тепло — это процессы, , которые добавляют или вычитают энергию, в то время как внутренняя энергия U {\ displaystyle U} представляет собой конкретную форму энергии , связанную с системой. Таким образом, термин «тепловая энергия» для δQ {\ displaystyle \ delta Q} означает «количество энергии, добавляемой в результате нагрева», а не относится к конкретной форме энергии.Точно так же термин «рабочая энергия» для δW {\ displaystyle \ delta W} означает «количество энергии, потерянное в результате работы». Наиболее значительным результатом этого различия является тот факт, что можно четко указать количество внутренней энергии, которой обладает термодинамическая система, но нельзя сказать, сколько энергии поступило в систему или из нее в результате ее нагрева или охлаждения. , ни в результате работы, выполняемой системой или ею. Проще говоря, это означает, что энергия не может быть создана или уничтожена, а только преобразована из одной формы в другую.

Для простой сжимаемой системы работа, выполняемая системой, может быть записана в виде

δW = PdV {\ displaystyle \ delta W = P \, \ mathrm {d} V},

где P {\ displaystyle P } — давление, а dV {\ displaystyle dV} — небольшое изменение объема системы, каждая из которых является системными переменными. Тепловая энергия может быть записана в виде

δQ = TdS {\ displaystyle \ delta Q = T \, \ mathrm {d} S},

, где T {\ displaystyle T} — температура, а dS {\ displaystyle \ mathrm {d} S} — небольшое изменение энтропии системы.{N} p_ {i} {\ dot {q}} _ {i} -L = const} и pi = ∂L∂q˙i {\ displaystyle p_ {i} = {\ frac {\ partial L} {\ partial {\ dot {q}} _ {i}}}}

, где L — функция Лагранжа. Чтобы эта конкретная форма была действительной, должно выполняться следующее:

• Система является склерономной (ни кинетическая, ни потенциальная энергия не являются явной функцией времени)
• Кинетическая энергия является квадратичной формой относительно скоростей
• потенциальная энергия не зависит от скоростей

Теорема Нётер

Сохранение энергии — общая черта многих физических теорий.С математической точки зрения это понимается как следствие теоремы Нётер, которая утверждает, что каждая симметрия физической теории имеет ассоциированную сохраняющуюся величину; если симметрия теории неизменна во времени, то сохраняющаяся величина называется «энергией». Закон сохранения энергии является следствием сдвиговой симметрии времени; Сохранение энергии подразумевается эмпирическим фактом, что законы физики не меняются с течением времени. С философской точки зрения это можно сформулировать как «ничто не зависит от времени как такового.» Другими словами, если теория инвариантна относительно непрерывной симметрии переноса времени, то ее энергия (которая является канонически сопряженной величиной времени) сохраняется. И наоборот, теории, которые не являются инвариантными относительно сдвигов во времени (например, системы с зависящей от времени потенциальной энергией), не демонстрируют сохранения энергии — если только кто-то не считает, что они обмениваются энергией с другой, внешней системой, так что теория расширенной системы становится снова инвариант времени. Поскольку любую изменяющуюся во времени теорию можно встроить в не зависящую от времени метатеорию сохранения энергии, всегда можно восстановить подходящее переопределение того, что такое энергия.Таким образом, сохранение энергии для конечных систем справедливо во всех современных физических теориях, таких как специальная и общая теория относительности и квантовая теория (включая квантовую электродинамику).

Относительность

В формулировке специальной теории относительности Альберта Эйнштейна было предложено, чтобы энергия была одним из компонентов 4-вектора энергии-импульса. Каждый из четырех компонентов (один энергии и три импульса) этого вектора отдельно сохраняется в любой данной инерциальной системе отсчета.Также сохраняется длина вектора (норма Минковского), которая является массой покоя. Релятивистская энергия одиночной массивной частицы содержит термин, связанный с ее массой покоя в дополнение к ее кинетической энергии движения. В пределе нулевой кинетической энергии (или, что то же самое, в системе отсчета покоя массивной частицы или в системе отсчета центра импульса для объектов или систем) полная энергия частицы или объекта (включая внутреннюю кинетическую энергию в системах) связана к его массе покоя с помощью знаменитого уравнения E = mc2 {\ displaystyle E = mc ^ {2}}.Таким образом, в специальной теории относительности было показано, что правило сохранения энергии является частным случаем более общего правила, альтернативно называемого сохранения массы и энергии, сохранения массы-энергии, сохранения энергии. -momentum, сохранение инвариантной массы, или теперь обычно именуется просто сохранения энергии.

В общей теории относительности сохранение энергии-импульса выражается с помощью псевдотензора энергии-импульса.

Квантовая теория

В квантовой механике энергия определяется как пропорциональная производной волновой функции по времени. Отсутствие коммутации оператора производной по времени с самим оператором времени математически приводит к принципу неопределенности для времени и энергии: чем больше период времени, тем точнее может быть определена энергия (энергия и время становятся сопряженной парой Фурье).

Однако существует глубокое противоречие между исторической оценкой квантовой теорией плотности энергии вакуума во Вселенной и энергией вакуума, предсказываемой космологической постоянной.Расчетная разница в плотности энергии составляет порядка 10 ¹²⁰ раз. Развивается консенсус о том, что квантово-механическая полученная плотность энергии нулевого поля не сохраняет полную энергию Вселенной и не соответствует нашему пониманию расширения Вселенной. За кулисами физики прилагаются интенсивные усилия, чтобы разрешить эту дилемму и привести ее в соответствие с расширяющейся Вселенной.

См. Также

• Теория хаоса
• Термодинамика
• Принцип неопределенности
• Закон сохранения
• Сохранение массы
• Энергетический баланс подземных вод
• Законы термодинамики
• Теорема Нётер
• Принципы энергетики
• Преобразование энергии
Качество энергии

Примечания

1. ↑ A.Л. Лавуазье, П.С. Лаплас, Воспоминания о тепле, Королевская академия наук (1780): 4-355.
2. ↑ J.R. von Mayer, Замечания о силах неорганической природы, Annalen der Chemie und Pharmacie 43 (1842): 233.
3. ↑ W.R. Grove, The Correlation of Physical Force, 6-е изд. (Лондон, Великобритания: Longmans, Green, 1874 г.).

Каталожные номера

• Brown, T.M. 1965. Информационное письмо EEC-1 об эволюции энергетических концепций от Галилея до Гельмгольца. Американский журнал физики . 33: 759–765.
• Cardwell, D.S.L. 1971. От Ватта до Клаузиуса: подъем термодинамики в раннюю индустриальную эпоху . Лондон, Великобритания: Heinemann. ISBN 0435541501.
• Колдинг, Л. А. 1864. К истории принципа сохранения энергии. Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 27: 56–64.
• Гольдштейн, Мартин и Ф. Инге Ф. 1993. Холодильник и Вселенная .Кембридж, Массачусетс: Гарвардский унив. Нажмите. ISBN 9780674753242.
• Guillen, M. 1999. Пять уравнений, которые изменили мир . Лондон, Великобритания: Abacus. ISBN 034
• 46.
• Hiebert, E.N. 1981. Исторические корни принципа сохранения энергии . Мэдисон, Висконсин: Ayer Co Pub. ISBN 0405138806.
• Кремер, Герберт и Чарльз Киттель. 1980. Теплофизика, 2-е изд. Сан-Франциско, Калифорния: W.H. Компания Freeman. ISBN 0716710889.
• Kuhn, T.С. 1957. «Энергосбережение как пример одновременного открытия». В М. Клагетте (ред.), Критические проблемы истории науки . Мэдисон, Висконсин: University of Wisconsin Press.
• Ланцош, Корнелиус. 1970. Вариационные принципы механики . Торонто, Калифорния: Университет Торонто Press. ISBN 0802017436.
• Мах, E. 1872. История и корни принципов сохранения энергии . Анн-Арбор, Мичиган: Международный университет микрофильмов.
• Нолан, Питер Дж. 1996. Основы физики в колледже, 2-е изд. Дубьюк, ИА: Издательство Уильяма С. Брауна. ISBN 9780697121455.
• Oxtoby, David W. и Norman H Nachtrieb. 1996. Принципы современной химии, 3-е изд. Форт-Уэрт, Техас. Издательство колледжа Сондерс. ISBN 9780030059049.
• Папино, Д. 2002. Размышляя о сознании . Оксфорд, Великобритания: Издательство Оксфордского университета. ISBN 9780199271153.
• Пуанкаре, Х. 1905. Наука и гипотеза .Нью-Йорк, Нью-Йорк: переиздание Дувра, 1952. ISBN 0486602214.
• Сартон, Г. 1929. Открытие закона сохранения энергии. Исида 13: 18–49.
• Serway, Raymond A. и John W. Jewett. 2004. Физика для ученых и инженеров, 6-е изд. Бельмонт, Калифорния: Брукс / Коул. ISBN 0534408427.
• Смит, С. 1998. Наука об энергии: Культурная история физики энергетики в викторианской Британии . Лондон, Великобритания: Heinemann. ISBN 0485114313.
• Stenger, Victor J.2000. Вневременная реальность . Амхерст, Нью-Йорк: Книги Прометея. ISBN 9781573928595.
• Типлер, Пол. 2004. Физика для ученых и инженеров: механика, колебания и волны, термодинамика, 5-е изд. Сан-Франциско, Калифорния: W.H. Фримен. ISBN 0716708094.

Credits

New World Encyclopedia писатели и редакторы переписали и завершили статью Wikipedia в соответствии со стандартами New World Encyclopedia .