Счет десятками — 14 ответов
В начальных классах школы одной из главных задач в освоении математики — является правильное формирование представления у детей понимания числового ряда и понимания десятичного состава числа.
Для этого сначала обязательно нужно объяснить, что каждое число в числовом ряду больше предыдущего на 1. Очень важно, чтобы ребенок умел считать от заданного числа до заданного в прямом и обратном порядке (например, от 2 до 9, от 12 до 5), знал место каждого числа в числовом ряду. Необходимо усвоить, что когда предметов мало, то их считают по одному, а когда предметов много, их группируют при счете, например, парами, пятками, десятками.
Для усвоения счета десятками очень важно подробно остановиться на втором десятке, объяснить принципы образования двузначных чисел и ввести ребенка в основы позиционной десятичной системы счисления.
Давайте поможем нашим маленьким ученым усвоить эту тему.
— Как быстро узнать, сколько на столе палочек?
Если ребенок ничего не придумал, то предложите ему самостоятельно собрать палочки в пучки — десятки. Включитесь в эту работу, отсчитывайте вместе по 10 палочек и скрепляйте эти десятки при помощи резиночек. Когда все палочки собраны в десятки, вместе с учеником посчитайте их: 1 десяток, 2 десятка и так далее до 10 десятков. Хорошо бы выяснить, что эти десятки можно складывать и вычитать как простые единицы.
Для начала обучения нумерации чисел от 21 до 100 полезно использовать любые наглядные пособия,
среди которых особую роль играют счеты и абак — наглядное пособие в
виде лент с прорезями для цифр или знаков, их заменяющих, таблицы с
кармашками и т.
Счеты | Абаки | Таблица с кармашками |
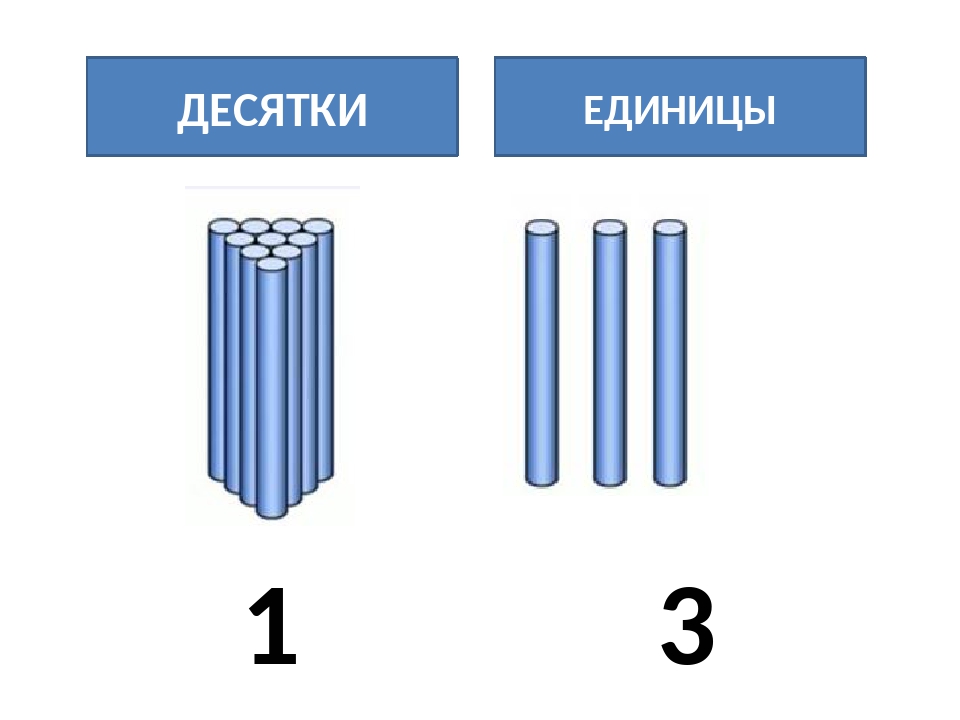
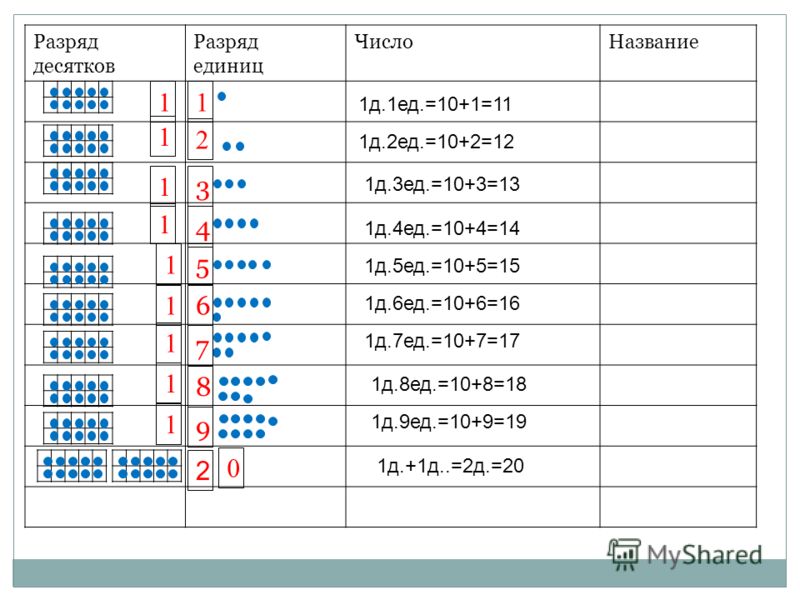
Например, рассмотрим, что изображено на рисунке с таблицей. В отделении десяток стоит 3 пучка палочек по 10 штук, то есть 3 десятка. В отделении для единиц стоит 4 палочки. Продемонстрируйте ребенку и спросите его: «Сколько десятков? (3.) Какое это число? (30.) Сколько единиц? (4.) Какое число изображено на полотне? (34.) » Точно такие же манипуляции можно сделать и на счетах и на абаках. Все это помогает усваивать десятичный состав чисел.
Чтобы показать, как образуются числа 20, 30, …, полезно использовать счеты. Сначала нужно пересчетом показать, что на одной проволоке 10 косточек (это 1 десяток), затем, считая десятками, показать сколько всего десятков косточек на счетах.
Теперь ребенок должен сам отложить на
счетах, например, 2 десятка косточек, а мы его должны спросить: «Сколько
всего отдельных косточек отложено?» Ответ: 20 косточек.
Следующее задание:
— Прибавь еще 1 десяток. Сколько теперь десятков отложено? (Ответ: 3 десятка)
— Сосчитай теперь эти косточки по одной вслух, прибавляя их к предыдущим 20 (21, 22 и т.д. до 30)
Значит, 3 десятка — это 30 единиц. Можно записать на бумаге и еще раз озвучить вместе с нашим учеником.
Далее придвигаем еще десяток — получаем 4 десятка, прибавляем по одному от 30 и устанавливаем, что это 40 единиц.
Аналогично рассматриваем образование чисел 90, 100 (с прибавлением единиц к числу 90).
Уделите внимание решению простых примеров на сложение и вычитание десятков, например, 50+10=60. Проведите устный разбор примера: 5 десятков плюс 1 десяток, будет 6 десятков, или шестьдесят. Придумайте несколько примеров на сложение и вычитание и сделайте вывод: десятки можно считать, складывать, вычитать как простые единицы.
Наряду с палочками полезно использовать
еще одно пособие — «ленту ста» (швейный сантиметр).
Дело в том, что,
связав палочки в десятки, дети, в конечном счете, видят только 10
пучков, но не видят натурального ряда, не видят, какое место занимает в
этом ряду каждое круглое число. На «ленте ста», представляющей собой
метр, разделенный на сантиметры, дети могут посчитать сантиметры и по
одному, и десятками.
Еще одно задание, которое нужно выполнить с ребенком, показать переход через все круглые числа (30, 40, 50, 60, 70, 80, 90). Для этого нужно обратить особое внимание на называние чисел в прямом и обратном порядке с переходом через данное круглое число: 1) 37, 38, 39, 40, 41 … и 2) 73, 72, 71, 70, 69 … и т. д.
Чтобы окончательно усвоить и закрепить материал нашего занятия, уделим внимание правилу, по которому образуются названия круглых десятков и остальных двузначных чисел, а также исключениям из этого правила (40 и 90).
Большинство названий круглых десятков представляет собой сочетание известных детям названий однозначных чисел и сокращенного слова «-дцать» или «-десят»
вместо «десяток» (двадцать, тридцать, пятьдесят и т.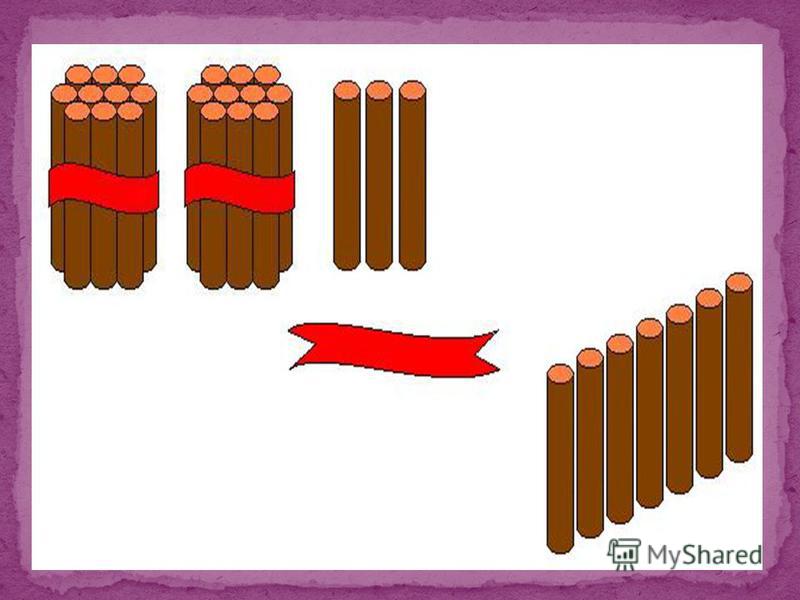
д.). Обсудите и
сопоставьте с ребенком эти названия с уже известными названиями чисел
второго десятка: тринадцать и тридцать, пятнадцать и пятьдесят и т. д.
Для названий круглых десятков
употребляют сложные имена числительные, обозначающие количество десятков в числе. Образование этих чисел происходит на основе умножения:30 = 3х10 = три-дцать = 3 раза по десять или три десятка.
Названия остальных двузначных чисел образуются на основе употребления составных имен числительных, состоящих из двух слов: первое слово обозначает разряд десятков, а второе — разряд единиц. Образование этих чисел происходит на основе умножения и сложения:
34 = 3х10 + 4 = три-дцать-четыре = 3 десятка да еще 4 единицы.
Письменная нумерация двузначных чисел строится на основе поместного значения цифр. Важно объяснить детям, что одна и та же цифра может иметь разное значение в записи числа в зависимости от места, которое она в этой записи занимает.
Во время занятия каждый новый вычислительный прием иллюстрируйте с помощью пучков палочек и отдельных палочек (или косточек на счетах), а также сопровождайте подробными пояснениями и записями с использованием письменных вычислений. Это помогает детям не только лучше понять и усвоить алгоритм вычислений, но и научиться рассуждать.
Приятно, когда ваш ребенок умеет осознанно и грамотно использовать математическую речь. Постарайтесь, как можно раньше, сформировать умение комментировать и обосновывать выполняемые действия, а для этого еще на этапе одношаговых рассуждений, можно использовать, например, при изучении письменных приемов сложения в пределах 100 можно использовать подобную схему рассуждений.
1) Записываю пример в столбик
2) Складываю единицы.
3) Складываю десятки.
4) Читаю ответ.
По мере того как прием будет усвоен, эти рассуждения можно постепенно сокращать. Например: «Десятки складывают с десятками, а единицы — с единицами; единицы вычитают из единиц, а десятки — из десятков». Такие пояснения будут даваться, например, при вычислении сумм вида 35 + 2, 60 + 34 или разностей вида 56 – 20, 56 – 2.
Проводя такие рассуждения, учащиеся лучше усваивают структуру объяснения вычислений и непосредственно сами приемы сложения и вычитания чисел в пределах 100.
Нужно научить и отработать умение выполнять проверку действий сложения и вычитания, которая включает как устные, так и письменные приемы вычислений.
Не торопите своих учеников, если у них возникли трудности в понимании
вычислительного приема или появились ошибки в вычислениях, то дайте
возможность вернуться к демонстрационным пособиям и не абстрактно, а на
наглядном и предметном уровне выполнить арифметические действия.
Этап | Ресурсы | Деятельность учителя | Деятельность учащихся | Оценивание | Модуль | ||||||||||||||||||||||||||
I. Мотивационный этап. | слайд слайд карточки Таблица на группу Слайд – проверка слайд | Тренинг «Комплимент» Эмоциональный настрой Каллиграфическая минутка Самооценка Повторение правил работы в группе и паре — Сегодня на уроке мы будем работать в парах, в группах. – Ребята, Незнайка прислал вам телеграмму, в которой дает вам совет. Вам, ребята, дам совет, – Ребята, полезный ли совет дал вам Незнайка? — Поэтому начинаем наш урок с взаимотренажа. Взаимотренаж – решение примеров в пределах 10 -Что вы сейчас делали в парах? — Для чего? -Оцените свою работу. Выход на тему урока. Математическая разминка -Чтобы определить тему нашего урока, нам предстоит решить числовые выражения. 9-2=к 2+7=м 4+4=а 10-10=и -О чём мы будем сегодня говорить? (Счёт десятками — на доске) Постановка целей и определение темы урока. Я узнаю… Я смогу… Я научусь… | Цель: формирование умения замечать положительные качества в людях и говорить им об этом Дети сидят в круге. Приветствуют друг друга и говорят что-нибудь приятное любому участнику группы. Если кто-то из детей не получил комплимент, то психолог его сам или просит об этом детей. Оценивание стикерами на светофоре Прописывают цифры Записывают число, классная работа Повторение правил работы в группе и паре (Текст телеграммы читает ученик.) Ответы детей. Работа в парах сменного состава Работа в группе считают, заполняют таблицу
Заполняют Табло успеха – Высказывания детей | «Светофор» зелёный – у меня хорошее настроение, жёлтый – ревожно, красный – я не хочу на урок Табло успеха самооценка Техника «20 секунд». | НП ОдО КМ УиЛ ВО ТиО ИКТ | ||||||||||||||||||||||||||
II. Операционный этап. | Счётный материал Конверты с десятками Слайд для проверки Слайд для проверки карточки | – Ребята, а что вы знаете о десятке, с точки зрения математики? -Чем отличается это число от других? (Два знака в записи) – это десять предметов; Моделирование — На прошлом уроке вы составили модель десятка — треугольник — Возьмите конверты с треугольниками. — Что обозначает один треугольник? (Один десяток) — Добавьте к нему другой треугольник. Что получилось? (Два десятка) — Какие действия производили? (Сложение) — Какие единицы счета использовали? (Десятки) — А какие действия можно выполнять с десятками? -Как нам выполнить действие вычитания? (убрать 1 десяток). Скажите, а где в жизни мы используем счет десятками? (яйца, пуговицы, тетради, таблетки…) Счёт десятками Составьте выражение, запишите значение выражение.
20 + 40 = 60
70 – 30 = 40 Оцените свою деятельность в группе физминутка Отработка счёта десятками
Оцените свою работу | Работа в группе. сложение вычитание (Десятки можно складывать и вычитать) Десятки складывают и вычитают, как обычные числа Работа в группе – проверка по образцу Выполняют на А4 Работа парами в тетрадях Проверка в группе Обмен карточками | Техника «20 секунд». Взаимопроверка «Сигналы рукой» | |||||||||||||||||||||||||||
III. Рефлексия. | Карточки | — Какое правило сложения и вычитания десятков вы узнали? (Круглые десятки складываются так же, как и единицы) Контроль А –Посчитай 20+30= 90-50= 40+30= 80-20= В – Реши задачу. В хоре поют 10 мальчиков и 30 девочек. Сколько всего детей в хоре? С – Решить уравнение. Х+30=70 — Какое затруднение у вас возникло? В чем была причина затруднения? — Кого вы сегодня хотите поблагодарить и за что? «Светофор» зелёный — всё было понятным, работой доволен жёлтый – понял, но хотел бы ещё поупражняться красный – было не интересно Д/з с. | Высказывания детей Индивидуальная работа Оценивание стикерами своей работы | ||||||||||||||||||||||||||||
№ 1 10+10= 10+20= 20-10= 30-10= | № 2 10+10= 20-10= 20+20= 40-20= | № 3 20+10= 10+20= 30-10= 30-20= | № 4 30+10= 10+30= 40-10= 40-30= | № 5 40+10= 10+40= 50-10= 50-40= | |||||||||||||||||||||||||||
№ 6 20+0= 0+20= 20-0= 20-20= | № 7 10+0= 0+10= 10-0= 10-10= | № 8 30+0= 0+30= 30-0= 30-30= | № 9 40+0= 0+40= 40-0= 40-40= | № 10 50+0= 0+50= 50-0= 50-50= | |||||||||||||||||||||||||||
№ 11 50+10= 10+50= 60-10= 60-50= | № 12 40+20= 20+40= 60-20= 60-40= | № 13 60+0= 0+60= 60-0= 60-60= | № 14 30+30= 60-30= 40+40= 80-40= | № 15 70+0= 0+70= 70-0= 70-70= |
Какие правила работы помогут нам достигнуть успеха?
Сколько стало? (3 десятка). Какое действие выполняли? (вычитание) Уберите ещё 1 треугольник. Сколько осталось? (2 десятка). Какое действие выполняли? (вычитание) 
186 № 2 примеры или № 3 уравнения по выбору19 Счет до 10 Упражнения – Знакомство, Практика, Применение – Раннее обучение
Счет до 10 – очень важный навык в жизни.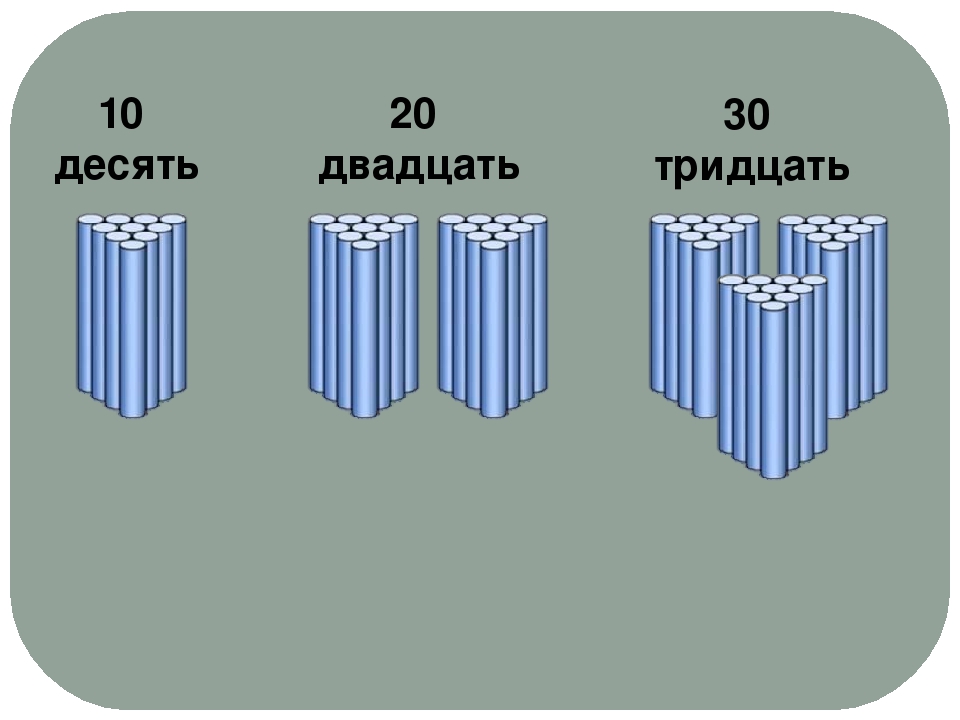
Чтобы научить детей этому навыку самым быстрым и эффективным способом, разумно пройти три этапа.
Проще говоря, начните с самых простых занятий, где детей обучают механическому счету десятками.
Затем перейдите к занятиям, где дети видят числа и произносят их. На этом этапе их практикующий навык.
Третий этап — начать думать десятками. Это помогает детям применять свои способности считать десятками и связывать их с практическими ситуациями.
За почти двенадцать лет обучения маленьких детей я пришел к выводу, что лучше всего следовать этому плану, а также обнаружил, что существует множество упражнений, наиболее эффективных для обучения этому навыку.
Для этой статьи я выбрал 19 лучших упражнений, которые я когда-либо выполнял, чтобы научить считать до 10.
They are:
| Beginning/Introducing | Count Marching |
| Action Counting | |
| Rote Counting | |
| Dance Counting | |
| Online Songs | |
| Счет разными голосами | |
| Упражнения в счете до 10 | Настольные игры |
| Знакомство с цифрой | |
| ОБЪЕКТЫ ЗАКАЗАЦИИ В 10S | |
| ЗАКАЗАЦИЯ НОМЕР | |
| ПРИПРЕДАТЬ | |
СКРЕЗОВЫЙ НОМЕР. Книги | |
| Надевание перчаток на бельевые веревки | |
| Подсчет групп детей | |
| Счетная палочка | |
| Запуск с числа, не являющиеся десяти | |
| Сетка вперед/назад | |
| Hit The Bulde Team Game |
Наши номера. пальцы.
Способность думать и считать десятками имеет много преимуществ, таких как сложение и вычитание в уме, оценка, решение задач и многое другое. (Источник)
Считать десятками весело! И дети будут наслаждаться этими играми, а также добиваться от них большого прогресса.
Я разделил эту статью на три уровня сложности — начальный, средний уровень сложности и затем применение навыка.
Хорошо, давайте начнем…
В этих первых играх дети знакомятся с концепцией счета десятками и механическим счетом. Это просто счет без предметов или визуальных эффектов — просто произнесение чисел по порядку.
(Если вы не знаете, что такое механический счет, сначала проверьте это).
1. Марширование на счет
В этих играх на механический счет определенно нужно быть как можно более активным, поэтому мы начнем с действительно физической игры.
Поднимите детей и маршируйте на месте.
Когда одна нога касается земли, все говорят «десять».
Затем «двадцать», когда приземляется следующая нога.
Продолжай в том же духе. Это хорошая идея, чтобы начать марш довольно медленно, но вы можете ускориться до нормального темпа марша, когда дети начнут хорошо петь десятками.
Примечание. Я всегда дохожу до 100, даже если вы просто достигаете 110. Многие дети думают, что цифры заканчиваются на 100, поэтому постарайтесь избежать этой ловушки!
2. Подсчет действий
Физическая идея похожа на подсчет маршей, и это хороший способ начать.
Просто выберите какое-нибудь движение, и все вместе начните его делать.
Это может быть:
- Прыжки
- Растяжка
- Потягивание в одну сторону, затем в другую
- Прыжки
Что-нибудь еще подобное тоже было бы здорово.
Просто выполните действие, говоря «десять». Затем повторите то же самое, сказав «двадцать» и так далее.
Продолжайте двигаться и считать
3. Механический счет
Вот простое занятие, которое занимает всего несколько минут и поэтому может выполняться в течение дня.
Это просто сесть вместе и повторять числа от 10 до 100.
Очень просто, но нужно немного этого, чтобы оживить другие игры.
4. Танцевальный счет
Смешение танца со счетом — отличный план, который отлично подходит для вовлечения и возбуждения детей.
Включите какую-нибудь зажигательную танцевальную мелодию. Хорошо использовать какую-нибудь поп-песню без слов, если вы сможете ее найти. Вот один, который вы можете использовать для YouTube, который нравится детям:
Включите зажигательную мелодию, а затем выберите какое-нибудь танцевальное движение.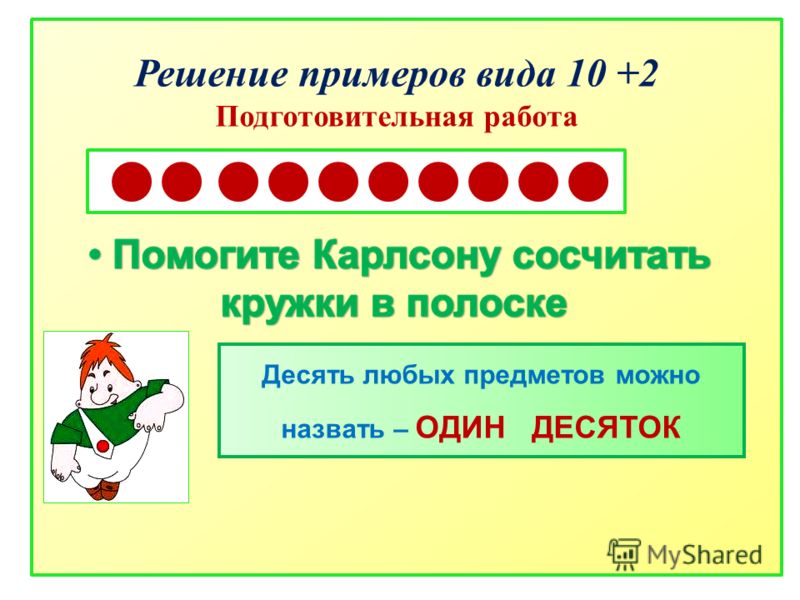
Это может быть что-то простое, например, вытянуть обе руки вправо, а затем обе влево. Или потянуться вверх, затем вниз, вверх, затем вниз.
Сделай это под музыку, а потом начни считать десятками!
Еще раз попытайтесь пройти дальше 100.
Затем выберите другое танцевальное движение и повторите процесс снова. Повторяйте с разными танцевальными движениями, всегда считая десятками.
5. Онлайн-песни
На YouTube есть несколько бесплатных песен, которые отлично подходят для счета десятками и которые очень нравятся детям.
Моим детям понравился вот этот:
6. Счет разными голосами
Это отличный способ вовлечь труднодоступных учеников или детей, которые просто не очень заинтересованы в счете.
Я использую для этого кубик, который выглядит так:
Впрочем, это не обязательно. Эта игральная кость представляет собой деревянный строительный блок, на котором я нарисовал шесть символов. Персонажи (хотя это не высечено на камне):
- Принцесса
- Робот
- Инопланетянин
- Тигр
- Мышь
- Призрак
Вам нужно бросить кубик и посмотреть, на каком символе он выпадет. Например, он может приземлиться на призрака.
Каждый будет использовать свой призрачный голос во время пения десятками!
Затем попросите другого ребенка бросить кости, и какой бы персонаж вы ни получили, попробуйте использовать этот голос.
Эта веселая игра включает в себя уровень воображения и ролевой игры, а также практику счета.
Когда дети освоят механический счет последовательностей чисел, пора приучать их одновременно смотреть на зрительные числа.
Хорошо вводить числовые линии в различных контекстах.
Это могут быть настольные игры, числовые линии на стене или полу, беговые дорожки на открытом воздухе, предметы, которые они могут заказать, и что-то еще в этом роде.
Давайте рассмотрим некоторые из лучших способов попрактиковаться в механическом счете, одновременно рассматривая числа:
7. Начало использования числовой строки
Это первое задание простое, но очень важное.
Проще говоря, покажите детям какую-нибудь числовую линейку и потренируйтесь прыгать по ней за 10 секунд.
Используемые типы числовой строки включают:
Длинная числовая строка до 100 – попрактикуйтесь в прыжках
Числовая строка из 10 – т.е. квадрат идет 10, 20, 30..
Хорошо, если дети познакомятся с рядом различных числовых линий, чтобы они могли визуализировать последовательности чисел по-разному.
Регулярная практика простого счета десятками на числовой прямой дает множество преимуществ.
8. Игра в настольные игры с цифрами 10
Это очень просто настроить.
Вам нужен какой-нибудь легкий «трек». Это может быть лист большой бумаги, например, обоев, с нарисованной на нем длинной прямоугольной линией.
Начните с 0 и поднимайтесь с 10, 20, 30 до 100 или даже 200.
Имейте несколько простых фишек — что-нибудь вроде разноцветных камней или кусочков лего.
Хорошая игра для 2-6 детей. У каждого ребенка есть свой счетчик, который он ставит на ноль.
Возьмите кубик и по очереди бросайте кубики, а затем прыгайте вперед на это число вдоль числовой линии.
Итак, если выпадет тройка, прыгайте вперед на три ящика – 10, 20, 30.
Затем следующий игрок имеет право.
Продолжайте по очереди бросать кости и двигаться. Чемпион – это тот, кто первым доберется до конца очереди.
9. Упорядочивание объектов в десятках
Детям полезно начать экспериментировать и строить свои собственные числовые последовательности с объектами в десятках.
Так что поместите кратное десяти на некоторые случайные объекты стиля незакрепленных частей.
Подойдет что-то вроде кусочков дерева (с цифрами — 10, 20, 30 и т. д.). Или вы также можете использовать что-то вроде:
- Крышки для бутылок
- Раковины
- Пробки
Или что-то еще, что вы можете найти в этом роде. Написание цифр перманентным маркером — лучший способ сделать это.
Затем попросите детей разложить их по порядку.
Они могут использовать какую-то линейку десятков или свои методы (для тех, кто умеет считать наизусть).
10. Заказ числовых камней
Числовые камни — прекрасный ресурс, который можно использовать для множества простых числовых действий.
Все, что вам нужно для этого, это несколько простых камешков. Напишите или нарисуйте на камнях числа, кратные десяти. Вот как выглядят мои десятки камней:
Я использую акриловую краску, так как она будет держаться на камнях практически постоянно. Для более быстрого результата используйте перманентный маркер, чтобы писать прямо на камнях. Вы можете установить камни с помощью ручки практически мгновенно.
С этими камнями можно делать так много всего, но самый простой способ — заказать их.
И снова дети могут использовать числовую линейку, если это необходимо. Однако, если они могут сделать это сами, вы можете увидеть, что у них в голове есть ряд десятков. Это именно то, что вы хотите!
11. Прыжки в десятки
Напишите на земле числа, кратные десяткам, в длинную строку.
Выстройте детей в линию рядом с нулем и скажите, что мы собираемся прыгать вдоль линии по одному, называя числа, на которые мы приземлились.
Тогда запускайте процесс! Первый ребенок прыгает по числовой строке, произнося числа – «10, 20, 30…»
Затем следует следующий ребенок и продолжает.
Потенциально вы могли бы провести разные числовые ряды по всему месту и продолжать прыгать и считать в любом месте, которое у вас есть.
12. Использование дорожек больших чисел снаружи
Это отличный способ исследовать числовую прямую действительно физическим и активным способом.
Все, что вам нужно, это кусок мела и большой кубик для этого.
Начертите на полу большую линию цифр – числа 0, 10, 20, по крайней мере до 100, в длинную линию. Сложите их в коробки, как дорожку в классики.
В эту игру могут играть от 2 до 4 игроков.
Один человек, взрослый или ребенок, который не играет, будет бросать кости.
Дети стоят в начале линии беговой дорожки. Решите, кто пойдет первым.
Бросьте кости и посмотрите, сколько шагов по числовой прямой прыгнет ребенок, например. 4. Они прыгают на 4 шага – «10, 20, 30, 40!»
Затем идет следующий ребенок.
Когда дети освоили механический счет десятками, а также связали этот навык с использованием числовых линий, настало время применить этот навык в различных контекстах.
Вот о чем эти следующие идеи.
13. Применение навыка в книгах
Некоторые книжки с картинками богаты возможностями для применения навыка счета десятками.
Один из них, который мне очень нравится, называется «Один — улитка, десять — краб».
Эта книга посвящена количеству ног у животных. Он начинается просто с улитки (с одной ногой), затем с человека (с двумя) и продолжается по номерам.
Десятка представлена крабом, потому что у краба, по-видимому, десять ног (если считать и клешни).
Ближе к концу книги есть много возможностей считать до 10.
Например, на этой странице:
Это действительно наглядный и увлекательный способ сделать счет на десять веселым и актуальным.
14. Повесить пару перчаток на бельевую веревку
Есть так много числовых навыков, которым можно научиться на бельевой веревке.
Пары перчаток — отличный способ применить навык счета десятками.
Все, что нужно сделать детям, это найти несколько пар перчаток и приколоть их друг к другу. Каждая пара (очевидно) будет иметь десять пальцев (считая большие пальцы).
Итак, если у вас есть четыре пары перчаток, то это «10, 20, 30, 40 пальцев».
15. Подсчет группы детей
Соберите небольшую группу детей и подумайте, сколько пальцев рук или ног у них будет в целом.
Итак, если трое детей встанут вместе, сколько у них будет детей? Потренируйтесь считать по 10, чтобы найти ответ.
В эту же игру можно играть со всем, что можно сосчитать за 10 секунд.
16. Используйте счетную палочку
Счетные палочки — еще один замечательный инструмент для развития различных навыков счета.
Все они представляют собой палку, похожую на ручку метлы или что-то подобное, с секциями на ней. Они выглядят так:
Вы можете потренироваться считать палочки вверх и вниз десятками, указывая на каждую секцию и предлагая детям последовательно называть числа.
17. Начинать с числа, отличного от 10
Как только дети научатся считать десятками от десяти, следующим шагом будет начать с другого числа.
Это значительно усложняет задачу, но им действительно полезно научиться делать это, и это важно для вычислений и арифметики в уме.
Один из способов сделать это — написать число, кратное десяткам, на чем-то вроде камней или ракушек и положить в сумку.
Выньте один камень – напр. «50». Попробуйте начать считать от 50 и обязательно превысьте 100.
Не просто! Это занимает несколько подходов, но это действительно хороший навык для изучения.
18. Пение в прямом/обратном направлении
Еще один навык для расширения навыков детей, умеющих считать в прямом и обратном порядке, заключается в том, чтобы научиться считать в обратном порядке.
Опять же, начните со стратегий механического счета – пение, марширование, выполнение действий, танец и т. д. Затем, когда они справятся с этим, перейдите к использованию числовой линии.
19. Командная игра «Ударь шарик»
Это забавная игра с числами, в которой участвуют команды детей и по одному шарику на команду.
Воздушные шары можно использовать для всех видов обучения, они отлично подходят для командной работы, сотрудничества и многих других навыков.
Дети встают в команду от 3 до 6 человек, у каждого по одному шарику.
Первый человек ударяет по шарику и говорит: «Десять».
Следующий ударяющий (это может быть кто угодно) говорит: «Двадцать». Следующий говорит: «Тридцать» и так далее.
Цель состоит в том, чтобы не дать воздушному шару удариться об пол, а также одновременно считать до десятков.
Заключительные мысли
К счастью, счет десятками — увлекательный процесс, и вы можете использовать всевозможные мультисенсорные подходы.
Используйте песни, песнопения, танцы, действия и все, что вы можете придумать, чтобы заинтересовать детей.
Если эта статья оказалась для вас полезной, вы оцените еще одну — «17 фантастических идей для обучения механическому счету».
Recent Posts
ссылка на Transient Art — определение, примеры, действияПереходное искусство — определение, примеры, действия
Переходное искусство развивает многие навыки: творчество, решение проблем, исследование.
Продолжить чтение
ссылка на 23 открытых игровых идеи23 открытые игровые идеи
Есть бесконечное количество идей для игр с пером.
Здесь мы изучаем установки и идеи!
Продолжить чтение
Почему мы считаем в ДЕСЯТКАХ. И все о понимании числа… | от Nilabh Nishchhal ✍🏻💡 | Аналитика Видья
Photo by Kolleen Gladden on UnsplashМы начинаем считать с 1 и доходим до десяти, а затем внезапно разум переходит в автоматический режим (подсознательно, конечно) и увеличивает счет в другом наборе из десяти чисел, то есть от 11 до 20, с 21 по 30 и так далее.
Если вы заметите, числа — универсальное явление. Они не меняются. Девять всегда будет после восьми, а 13 всегда будет перед четырнадцатью, какую бы систему счисления вы ни использовали для их представления. Тогда почему у нас так много разных систем счисления?
При внимательном рассмотрении вам придет в голову, что разные системы счисления представляют одни и те же числа в разных обозначениях, символах или цифрах. Таким образом, вся путаница связана с тем, как представлять конкретное число. Само по себе число всегда одно и то же, независимо от системы счисления.
С появлением электрических сигналов в компьютерах компьютеры начали мыслить в терминах 0 и 1. Они создайте все номера из репозитория только этих двух номеров (0 и 1). И, следовательно, у них есть система счисления, основанная на двух цифрах, следовательно, основание равно 2. И поскольку вычисления теперь основаны на этих двух цифры , следовательно, компьютеры теперь Цифровые Компьютеры.
Наиболее часто используемой системой счисления является индийско-арабская система счисления. Это система счисления, которую мы используем в повседневной жизни для счета, вычислений и математических операций.
Первый индийский спутник имени Арьябхаты. Автор ISRO — https://imagine.gsfc.nasa.gov/science/toolbox/missions/aryabhata.html, общественное достояние, https://commons.
wikimedia.org/w/index.php?curid=10082533Two Indian математики, разделенные веком, Арьябхата (476–550 гг. Н. Э.) И Брахмагупта ((ок. 59 г.).8 г. н.э. — ок. 668 г. н.э.). Арьябхата разработал систему обозначения разряда, а Брахмагупта ввел символ нуля. Эта система счисления вместе с концепцией нуля, разработанной индусами Индии, распространилась в близлежащие регионы благодаря коммерческой и военной деятельности. Купцы начали торговать по этой системе, так как она была проще, научнее и стабильнее. Он попал в Европу из Аравии, и они немного изменили символы и стали называть его арабскими цифрами. Они очень похожи на обозначения чисел санскрита-деванагари, которые до сих пор используются в Индии и Непале.
Но это не единственная используемая система счисления. Различные цивилизации внесли свой вклад в этом отношении и имели свою собственную систему счисления с различными обозначениями. Всех их можно разделить на две большие группы.
- Обозначения значений знаков
- Обозначения значений разрядов
Обозначения значений знаков
Как следует из названия, эти числа имеют «Знаки», а эти знаки имеют «Значения».
В обозначениях значений знаков знаки представляют значение, которое в сумме составляет представленное число. Одним из таких примеров являются римские цифры. Римскими цифрами CCLVII означает 257 (100+100+50+5+1+1).
Табличка с протоклинописными пиктографическими знаками (конец 4 тыс. до н.э.), Урук III. Автор работы MbztOwn, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=25834613Система значений знаков может показаться громоздкой, поскольку мы привыкли к более эффективным системам счисления, но они были первым шагом человечества к числам вообще. Давайте поймем это по этой древней истории.
Племя хотело пересчитать своих овец, а также записать количество овец, принадлежащих разным людям в племени. Они сделали фигурку в виде овцы на глиняной табличке, изображающую одну овцу, а две фигурки овец изображают двух овец.
Но вот пришел один человек с 24 овцами, и записать его количество, отмечая фигурки овец, как раньше, было невозможно. Поэтому они создали еще один символ, который представляет 10 овец (почему 10? Мы обязательно ответим). И точно так же, как и когда количество стада овец продолжало увеличиваться, они продолжали изобретать новые символы для 50 овец, 100 овец и так далее. Возможно, это была первая запись значений знаков, использовавшаяся в качестве чисел, примерно в 4500–400 годах до нашей эры в месопотамской цивилизации (современный регион Ирак-Сирия-Иран).
Теперь, после прочтения этого, такой подход звучит вполне логично. Но по мере того, как люди по всему миру продолжали развиваться, менялись и их интеллектуальные потребности, и система счисления.
Обозначения разрядных значений (также известные как позиционные обозначения)
Как видно из названия, «место» числового обозначения определяет его «значение». Давайте посмотрим два примера.
В разрядной системе есть системы счисления с разными основаниями, которые мы вскоре рассмотрим. Но давайте сначала разберемся, что такое база . База — это не что иное, как «количество уникальных символов», которое имеет конкретная система счисления. Таким образом, для системы счисления с основанием 10 существует десять уникальных символов (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9). И, следовательно, производная от слова Дека (что означает 10), эта система называется Десятичной системой . Аналогично, для Двоичная система , основание равно 2, поэтому уникальных символов всего два (0 и 1).
Изображение числа с основанием 10, показывающее различные аспекты, такие как индекс, цифры и основание. Источник: Создано Автором.
Индийско-арабская система счисления (десятичная система) — наиболее часто используемая система счисления с основанием 10, но не самая старая. Первой позиционной системой счисления была вавилонская система счисления с основанием 60. Ее влияние ощущается во многих аспектах и сегодня. 60 минут в часе, 360 градусов угла в круге взяты из этой системы с основанием 60.
Это возвращает нас к исходному вопросу, с которого мы начали. Почему мы считаем десятками? Или почему десятичная система счисления имеет основание 10?
Эйнштейн считает на пальцах. https://martinlakewriting.files.wordpress.com/2013/11/einstein-counting-on-fingers.jpgВспомните самый распространенный способ счета, которым мы пользуемся, когда у нас нет другого аппарата. Наши пальцы. А сколько пальцев у нас на руках?
Десять…
Теперь понятно. Не случайно большинство мировых систем счисления, многие из которых разрабатывались независимо, имеют основание 10.
Для чтения разрядной системы счисления применим следующий метод.
Это верно для системы счисления любого числа в качестве основы.
Это станет яснее, когда мы вскоре увидим простые примеры преобразования для различных систем счисления.
Список систем счисления. В Википедии, свободной энциклопедии. Получено 10:22, 10 февраля 2021 г., с https://en.wikipedia.org/w/index.php?title=List_of_numeral_systems&oldid=1005801737Для цифровых вычислений существуют четыре основные системы счисления. Все они являются позиционными системами счисления или системами счисления Place Value.
1. Двоичная система счисления (основание 2)
2. Восьмеричная система счисления (основание 8)
3. Десятичная система счисления (основание 10)
4. Шестнадцатеричная система счисления (основание 16)
В цифровом формате В электронике и математике система счисления с основанием два известна как двоичная (би означает 2) система счисления. Это наиболее часто используемая система счисления во всех современных компьютерах из-за простой реализации цифровых электронных схем с использованием логических вентилей.
Эта система счисления с основанием 2 представляет собой позиционную запись с двумя символами, обычно «0» (ноль) и «1» (единица). Каждая цифра называется битом (это сокращение от двоичной цифры).
чисел в десятичном формате и эквивалентные им двоичные числа. Источник: создано автором. Этот счетчик показывает, как считать в двоичном формате от нуля до тридцати одного. Автор Ephert — собственная работа, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=38752676Двоичное число можно преобразовать в десятичное и наоборот. Счетчик слева показывает, как десятичное число представляется в двоичном формате. Потратьте время, чтобы понять это. Обратите внимание, как числа в средней строке соответствуют значениям десятичных чисел, когда добавляются соответствующие двоичные числа в третьей строке.
Например, 14 можно записать как 1110 в двоичном формате. Давайте посмотрим, как получить его значение, используя формулу, которую мы видели выше.
Почему двоичный код важен для цифровых вычислений?
Со времен электромеханических компьютеров до современных электронных компьютеров все они работают на электрических сигналах.
Электрический сигнал имеет два параметра: напряжение (вольт) и ток (ампер). Могут быть тысячи значений этих двух, и, следовательно, будет очень сложно присвоить числа различным значениям Вольта и Ампера для понимания компьютером. Чтобы упростить задачу, компьютеры используют только два значения: ON и OFF. ON равно 1, а OFF равно 0. Следовательно, двоичная система счисления подходит компьютерам или любой цифровой машине для хранения, передачи и обработки данных.
Не только цифры, текст и спец. символы также представлены в двоичном формате для понимания компьютером.
Поскольку это система счисления с основанием 8, она имеет 8 цифр или символов (0, 1, 2, 3, 4, 5, 6 и 7). Восьмеричные числа обычно используются в компьютерных приложениях. На заре компьютеров восьмеричная система счисления была очень популярна для подсчета входных и выходных данных, потому что, поскольку она работает в счете до восьми, входы и выходы были в счете восемь, байт (один байт = 8 бит) за раз.
Восьмеричная система счисления обеспечивает удобный способ преобразования очень длинных строк двоичных чисел в более компактные и меньшие группы. Однако в настоящее время восьмеричная система счисления почти исчезла и уступила место более эффективной шестнадцатеричной системе счисления.
Теперь вы знакомы с базой. Шестнадцатеричная система счисления — это 16-основная система счисления. В отличие от десятичной системы счисления, к которой мы привыкли в повседневной жизни, она имеет 16 различных символов или цифр.
Шестнадцатеричные числа не так часто используются в обычной математике, но они очень любимы проектировщиками компьютерных систем и программистами. Это просто потому, что они обеспечивают удобный для человека способ представления громоздких двоичных чисел. Каждая шестнадцатеричная цифра представляет четыре бита (двоичные цифры). Эти 4 бита называются полубайтом, а 8 бит составляют байт. Давайте посмотрим, как двоичное преобразование в шестнадцатеричное упрощает задачу.
Математика является универсальным языком и не зависит от используемой системы счисления. В принципе это звучит здорово, но люди не смогли бы стать такими продвинутыми в физике и других прикладных науках, если бы не было «ноля» (0). Сегодня мы воспринимаем Zero как должное, но так было не всегда. В системах счисления Sign Value нет нуля. Даже системы счисления, основанные на значениях, веками существовали без нуля.
Для цифровых компьютеров предпочтительна двоичная система счисления. Он так хорошо подходит, что хотя компьютерные системы изменились во всех других аспектах, от электромеханических к электрическим (на основе вакуумных ламп) и к электронным (на основе полупроводников), но для основного языка компьютера. Основной язык, который первые цифровые компьютеры понимали десятилетия назад, все тот же — двоичная система счисления. Следовательно, становится обязательным изучать и знать двоичный код. Десятичный язык является предпочтительным для людей из-за его простоты и стабильности, и, будучи забитым нулем, он пережил все другие системы счисления (их было много, которые мы здесь не обсуждали).
Сейчас он настолько широко используется, что стал синонимом «числа», и большинство людей не осознают, что это лишь одна из многих систем счисления.
При чем здесь восьмеричные и шестнадцатеричные числа?
Как восьмеричная, так и шестнадцатеричная системы счисления были связующим звеном между используемой компьютерами системой счисления (двоичной) и системой счисления, используемой человеком (десятичной). Для больших чисел в десятичной системе двоичное представление становится слишком большим, чтобы люди могли его запомнить или воспроизвести. Следовательно, чтобы сократить их вдвое, пригодится восьмеричная система. Идя еще дальше, шестнадцатеричная система сократила четыре бита до одной шестнадцатеричной цифры, уменьшив размер до одной четверти двоичного числа. Интересно отметить, что для всех систем счисления существуют арифметические операции, точно так же, как мы привыкли к десятичным. Но давайте закончим его той мыслью, что нам нужно понять, почему существуют другие системы счисления, кроме десятичной, и чем они полезны, как мы только что видели.